Maths
- 45 -
Les brevets
Sujets
Corrigés
Brevets blancs
© The scientific sentence. 2010
|
Mathématiques: Les brevets
Brevet des collèges
Madagascar
juin 2005.
Activités numériques
Exercice 1
1.
A = (3/4 - 3)/(1/2 + 2)
A = (- 9/4)/(5/2) = (- 9/4) x (2/5) = (- 9 x 2)/(4 x 5) =
(- 9)/(2 x 5) = - 9/10.
2.
B = (1.5 x 10-3)/(3 x 102)
a) Écriture décimale de B:
B = (1.5/3) x 10-3 - 2) = (1.5/3) x 10- 5) =
(15/3) x 10- 6) =
5 x 10-6 = 0.000005.
B = 0.000005.
b) B en écriture scientifique:
B = 5.0 x 10- 6
3.
a) C = √180 - 2√80
C = √(36 x 5) - 2√(16 x 5) =
6√5 - 8√5 = - 2√5
b) D = 5√12/2√3
D = 5√(3 x 4)/2√3 = 10√3/2√3 =
10 /2 = 5.
Exercice 2
1.
M = (3x + 5)2 - (3x + 5)(2x + 7)
1. M = 9x2 + 30x + 25 - (6x2 + 21x + 10x + 35) =
9x2 + 30x + 25 - 6x2 - 31x - 35 =
3x2 - x - 10.
M = 3x2 - x - 10
2. (3x + 5)2 - (3x + 5)(2x + 7) =
(3x + 5)[(3x + 5) - (2x + 7)] =
(3x + 5)[3x + 5 - 2x - 7] =
(3x + 5)(x - 2)
M = (3x + 5)(x - 2)
3.
M(x = 2) = (6 + 5)(2 - 2) = 0
M(x = 0) = (0 + 5)(0 - 2) = (5)(- 2) = - 10.
M(2) = 0
M(0) = - 10
4.
M = 0 si (3x + 5) = 0 ou (x - 2) = 0.
C'est à dire x = -5/3 ou x = 2
M = 0 si et seulement si x = - 5/3 ou x = 2.
Exercice 3
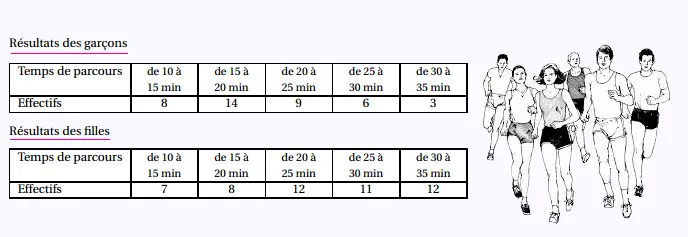
1.
a. Le temps de parcours moyen des garçons
est:
Mg = [8(10 + 15)/2 + 14(15 + 20)/2 + 9(20 + 25)/2 +
6(25 + 30)/2 + 3(30 + 35)/2]/40 =
[4 x 25 + 7 x 35 + 4.5 x 45 +
3 x 55 + 1.5 x 65]/40 = 20.25
Temps moyen pour les garçons = 20.25 mn = 20 mn 15 s.
b. Le temps de parcours moyen des filles
est:
Mf = [7(10 + 15)/2 + 8(15 + 20)/2 + 12(20 + 25)/2 +
11(25 + 30)/2 + 12(30 + 35)/2]/50 =
[3.5 x 25 + 4 x 35 + 6 x 45 +
5.5 x 55 + 6 x 65]/50 = 23.8
Temps moyen pour les filles = 23.8 mn = 23 mn 48 s.
2.
Voici le diagramme à bandes (qu’on appelle aussi diagrammes à barres ou histogrammes) relatif à la course des élèves:
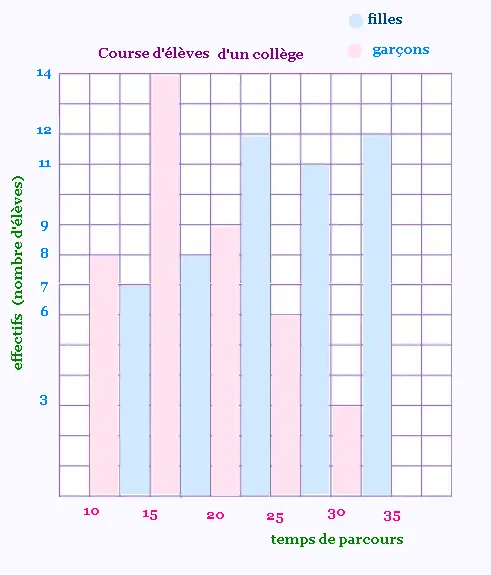
3.
a. Le nombre de garçons ayant effectué un temps
compris entre 15 et 30 minutes est égal à 14 + 9 + 6 = 29.
Le pourcentage correspondant est:
29/40 = 0.725 = 72.5%.
b. Le nombre de filles ayant effectué un temps
compris entre 15 et 30 minutes est égal à 8 + 12 + 11 = 31.
Le pourcentage correspondant est:
31/50 = 0.62 = 62%.
c. Le nombre d'élèves ayant effectué un temps
compris entre 15 et 30 minutes est égal à 29 + 31 = 60.
Le pourcentage correspondant est:
60/90 = 2/3 = 0,6667 = 66.67% = 66.7%.
4.
Les effectifs pour les garçons ne sont pas
sensiblement les mêmes (3 est loin de 14).
ce qui n'est pas le cas des filles.
On en conclu donc que le groupe des garçons
est plus dispersé que celui des filles, et donc
moins homogène.
Pour le groupe des garçons, l'étendue est égale à
eg = 14 - 3 = 11
Pour le groupe des filles: l'étendue est égale à
ef = 12 - 7 = 5
ef < eg : le groupe de filles est le plus homogène.
Activités géométriques
Exercice 1
1.
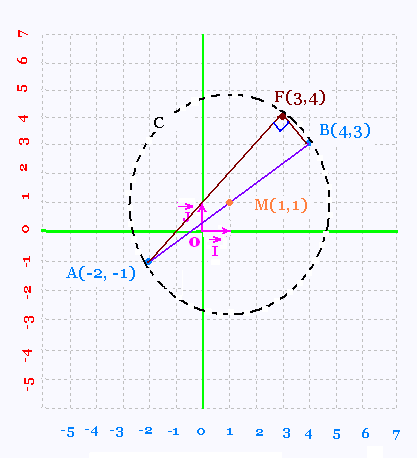
2.
M (x, y) est le centre du cercle, donc AM = MB.
D'où:
x + 2 = 4 - x et
y + 1 = 3 - y
Donc x = 1 et y = 1
M(1, 1)
3.
AM est le rayon du cercle.
AM(1 + 2, 1 + 1) = (3,2). Donc:
AM2 = 32 + 22 = 9 + 4 = 13.
Rayon du cercle = AM = √13.
4.
F(3,4) donne MF( 3 - 1, 4 - 1) = (2,3).
Donc MF2 = 22 + 32 =
4 + 9 = 13. D'où MF = √13.
Ainsi:
AM = MB = MF = √13 = rayon du cercle C.
Le point F se situe sur le cercle.
5.
[AB] est le diamètre du cercle, F est un point
sur le cercle, donc l'angle F est droit. Par
conséquent le triangle AFB est rectangle en F.
6.
FA = √50 et FB = √2
tg(∠FAB) = FB/FA = √2/√50 =
√(1/25) = 1/5 = 0.2.
tg-1(0.2) = 11°
mes(∠FAB) = 11°
On peut calculer cette mesure par le
cosinus. On a:
FA = (3 + 2, 4 + 1) = (5,5)
FA2 = 52 + 52 = 2 x 52
D'òu AF = 5√2.
AB(4 + 2,3 + 1) = (6, 4)
AB2 = 62 + 42 = 36 + 16 =
52
D'òu AF = 2√13
cos(∠FAB) = FA/AB = 5√2/2√13 =
= 1/5 = 0.98.
cos-1(0.98) = 11°
Exercice 2
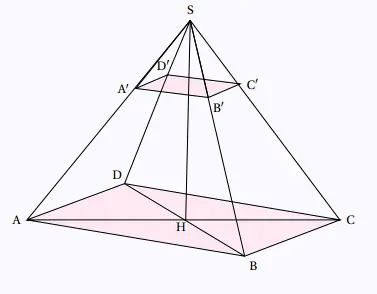
La pyramide SABCD est droite puisque sa hauteur SH issue
de l'apex S est perpendiculaire au centre de sa base
régulière rectangulaire.
AB = 8 cm, BC = 6 cm et SH = 12 cm.
1.
ABCD est un rectangle, donc ABC est un triangle droit.
D'après la règle de Pythagore:
AC2 = AB2 +
BC2 = 82 + 62 =
64 + 36 = 100.
Donc AC = 10 cm.
AC = 10 cm.
2.
Volume de la pyramide SABCD = aire de base x hauteur/3 =
AB x BC x SH/3 = 8 x 6 x 12 /3 = 192 cm3.
Volume de la pyramide SABCD = 192 cm3.
3.
Puisque les diagonales d'un rectangle se coupent
en leurs milieux,[AH] est la moitié de [AC]. Donc
AH = AC/2 = 10/2 = 5 cm.
AH = 5 cm.
La pyramide est droite, donc le triangle SHA est rectangle
en H. D'après le théorème de Pythagore:
SA2 = SH2 + AH2 =
122 + 52 = 144 + 25 = 169 =
132.
Donc SA = 13 cm.
SA = 13 cm.
On donne SA' = 3.25 cm.
On coupe la pyramide par le plan parallèle à la base
et passant par A'. On obtient une petite pyramide SA'B'C'D'.
4.
a)
La section A'B'C'D' est parallèle à la base ABCD.
Les droites (AS) (BS) et (CS) sont concourantes en S.
Le théorème de Thalès s'ecrit:
SA'/SA = SB'/SB = A'B'/AB
SB'/SB = SC'/SC = B'C'/BC
Le coefficient de réduction de SA'B'C'D' par rapport à
SABCD est `gal à SA'/SA = 3.25/13
b) Donc:
A'B'/AB = 3.25/13. D'où A'B' = (3.25/13) x AB =
(3.25/13) x 8 = 26/13 = 2
A'B'= 2 cm.
B'C'/BC = 3.25/13. D'où B'C' = (3.25/13) x BC =
(3.25/13) x 6 = 19.5/13 = 1.5
B'C''= 1.5 cm.
Volume de la pyramide SA'B'C'D' = (3.25/13)3 x Volume de la pyramide SABCD =
(3.25/13)3 x 192 cm3
= 3 3.
Volume de la pyramide SA'B'C'D' = 3 cm3.
5.
Pour obtenir une pyramide SA'B'C'D' dont le volume est huit
fois plus petit que celui de la pyramide SABCD, on doit
avoir:
(Volume de SA'B'C'D')/(Volume de SABCD) = 1/8
C'est à dire:
(SA'/SA)3 = 1/8. D'où:
SA'/SA = 1/2, donc SA' = 13/2 = 6.5 cm.
SA' = 6.5 cm.
Problème
1.
2.
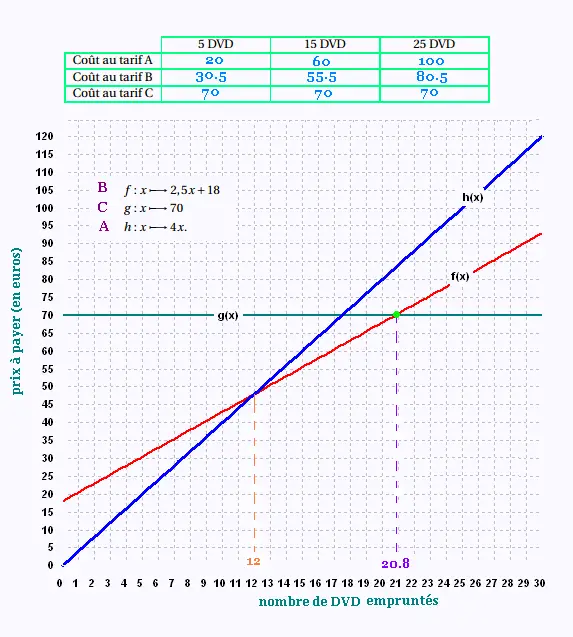
3.
a)
4x = 2.5x + 18
1.5 x = 18
x = 18/1.5 = 12.
x = 12.
b) Pour 12 DVD empruntés, les tarifs A et B donnent
le même prix à payer.
4.
a)
Le graphique donne:
Pour tout y = 2.5x + 18 ≥ 70
correspond un x ≥ 21.
L'ensemble des solutions de l'inéquation est donc:
S = {x: x≥ 21}.
b)
70 ≤ 2.5x + 18
70 - 18 ≤ 2.5x
52 ≤ 2.5x
d'où x ≥ 52/2.5 = 20.8
x ≥ 20.8.
S = {x: x≥ 28.8}.
4.
Jusqu'à 12 DVD empruntés, le tarif A est avantageux.
Entre 12 et 21 DVD, le tarif B est avantageux.
À partir de 21 DVD, c'est le tarif C qui est le plus avantageux.
Ici, avantageux signifie: payer moins.
|
|