Mathématiques: Le brevets

Brevet des collèges
Académie de Nancy-Metz juin 2000.

Activités numériques

Exercice 1

630 = 2 x 3² x 5 x 7
924 = 2² x 3 x 7 x 11

pgcd(630,924) = 2 x 3 x 7 = 42

630/924 = 3 x 5/2 x 11 = 15/22.

Exercice 2

A = (3/4) + (5/4)x(7/15) = (3/4) + (1/4)x(7/3) =
(3/4) + (7/12) = (9/12) + (7/12) = (9 + 7)/12 = 16/12 = 4/3

A = 4/3

B = (5/6 - 5/4) / (5/8) = (10/12 - 15/12) / (5/8) =
(- 5/12) / (5/8) = (- 5/12) x (8/5) = (- 1/12) x (8/1) = (- 8/12) = - 2/3

B = - 2/3

C = 8 x 10¹⁵ x 15 x 10^-6/20 x (10²)⁵ =
(8 x 15 /20) x 10^{15 - 6} /(10¹⁰) =
6 x 10^{15 - 6 - 10} = 6 x 10^{- 1} = 6/10 = 3/5

C = 3/5

Exercice 3

x: prix d'un cahier et
y prix d'un stylo.

3x + y = 57 $    (1)
5x + 3y = 107 $    (2)

L'équation (1) donne y = 57 - 3x

L'equation (2) devient:

5x + 3(57 - 3x) = 107

On développe:

5x + 171 - 9x = 107
- 4x + 171 = 107
4x = 171 - 107 = 64
x = 64/4 = 16

x = 16.

On substitue cette valeur de x dans l'une ou l'autre des équation (1) ou (2), on trouve:

y = 57 - 3 x 16 = 57 - 48 = 9

y = 9.

Ainsi

Un cahier coûte 16$ et un stylo coûte 9$.

Exercice 4

E = (2x + 3)² + (x - 7)(2x + 3).

a) E = 4x² + 12 x + 9 + 2x² + 3 x - 14 x - 21 =
6x² + x - 12

b) (2x + 3)(2x + 3 + x - 7) = (2x + 3)(3x - 4)

c) (2x + 3)(3x - 4) = 0 a pour solutions x = - 3/2 ou x = + 4/3.

d) si x √2, alors E = 6 x 2 + √2 - 12 = √2.

Activités géométriques

Exercice 1

AM = 6, MP = 4.8, AP = 3.6
EF = 6, AC = 4.5, AB = 7.5

1.
AM² = 6² = 36
MP² + AP² = (4.8)² + (3.6)² =
23.04 + 12.96 = 36.

AM² = MP² + AP². D'après la réciproque du théorème de Pythagore, the triangle AMP est rectangle en P.

2.
Les droites (EB) et (CF) sont sécantes en A.
Les droites (EF) et (MP) sont parallèles.
On applique donc le théorème de Thalès:

AM/AE = MP/EF . D'où : AE = AM x EF/MP =
6 x 6/4.8 = 36/4.8 = 7.5.

AE = 7.5

ME = AE - AM = 7.5 - 6 = 1.5

ME = 1.5

3.
AM/AB = 6/7.5 = 4/5
AP/AC = 3.6/4.5 = 4/5

On a donc AM/AB = AP/AC. D'après le théorème réciproqie de Thalès, les droites (MP) et (BC) sont parallèles.

3. Les droites (MP) et (BC) sont parallèles.
les droites (MB) et (PC) sont sécantes en A,

Donc les angles alternes internes &angla;CBA et ∠AMP sont égaux.

Exercice 2

1.


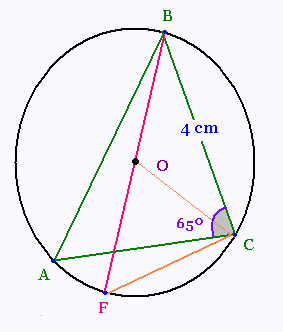
2.
[BF] est le diamètre du cercle. Le point C est sur le cercle.

D'après la propriété réciproque du triangle dans un cercle:

Si un triangle est défini par le diamètre d’un cercle et un autre point du cercle, alors ce triangle est rectangle ,

le triangle BFC est rectangle en C.

2. BF = diamètre = 2 x 3 cm = 6 cm.

sin(∠BFC) = BC/BF = 4/6 = 2/3

D'où : mes (∠BFC) = sin^-1(2/3) = 42°.

mes (∠BFC) = 42°.

4.
mes (∠FBC) = 90° - mes (∠BFC) =
90° - 42° = 48 °

Le triangle BOC est isocèles puisqu'il a deux côtés comme rayons d'un même cercle.

Ainsi mes (∠OCB) = mes (∠FBC) = 48°

Donc mes (∠BOC) = 180° - 2 x 48° = 84°.

Pour le triangle BOC:
mes (∠OBC) = 48°
mes (∠OCB) = 48°
mes (∠BOC) = 84°

Problème

Partie 1

On considère un cône de diamètre de base AB de 6 cm et de hauteur AS = 9 cm.

Le volume d'un cône de rayon de base r et de hauteur h est égal à (1/3) π r² x h.

1.
V = (1/3) π 3² x 9 = 27π cm².

2.
On verse un liquide dans le cône. Le liquide arrive à la hauteur SH et forme un disque de rayon HC.
a) HS = 4.5 cm :

On veut calculer le rayon HC du disque formé par le liquide.

Les droites (SB) et (SA) sont sécantes en S. Les disques de rayons respectifs AB et HC sont horizontaux, ainsi les droites (AB) et (HS) sont parallès.

On applique donc le théorème de Thalès et on trouve: SH/SA = HC/AB . D'où HC = AB x SH/SA = 3 x 4.5/9 = 3/2 = 1.5 cm.

HC = 1.5 cm.

b) Le volume du liquide à la hauter SH est :

(1/3) π (HC)² x SH = (1/3) π (1.5)² x 4.5 =
(1/3) π (9/4) x (9/2) = π (3/4) x (9/2) = (27/8)π cm³.

Le volume du liquide à la hauter SH = 4.5 cm est égal à (27/8)π cm³.

c) HS = x .

La relation de Thalès SH/SA = HC/AB trouvée en b) devient:

x/9 = HC/3. D'où HC = 3x/9 = x/3.

Le volume V du liquide correspondant est :

V = (1/3) . π . (x/3)² . x = (1/3) . π . x³/9 =
π . x³/27.

V = π x³/27 cm³ .

d) Avec HS = x = 3cm , V = π 3³/27 = π cm³

V = π cm³.

Avec HS = x = 6cm , V = π 6³/27 = π 2³ x 3³/27 =
π 2³ = 8π cm³

V = 8π cm³ .

Partie 2

On verse ensuite le liquide contenu dans le cône de volume V = (27/8)π cm³ dans un cylindre de même section de 6 cm de diamètre et de même hauteur 9 cm.

1.
Le volume total d'un cylindre de rayon de base r et de hauteur h est égal à πr² x h.

r = AB = 3 cm
h = AS = 9 cm

Ce volume est donc égal à π x 3² x 9 = 81 π cm³ .

Le volume total d'un cylindre est égal à 81 π cm³.

2.
Le volume du cône remplis à ras bord est 27 π cm³.

Pour remplir le cylindre de volume 81 π cm³ avec des cônes remplis à ras bord, il faut :

81 π cm³ /27 π cm³ = 81/27 = 3 x 27/27 = 3.

Le cylindre est l'équivalent de trois cônes de même section et de même hauteur.

3.
On désigne par y la hauteur en cm de liquide contenu dans le cylindre.

a) Le volume du liquide à la hauteur FG = y dans le cylindre est égal à: π . 3² . y = 9π y cm³ .

b) Si on verse un cône de liquide à la hauteur HS = x, donc de volume V = π x³/27 cm³ dans le cylindre, le volume équivalent dans le cylindre vaut: 9π y cm³. Ainsi:

π x³/27 cm³ = 9π y cm³. D'où :

x³/27 = 9 y , ou x³ = 27 x 9 y = 243 y

x³ = 243 y .

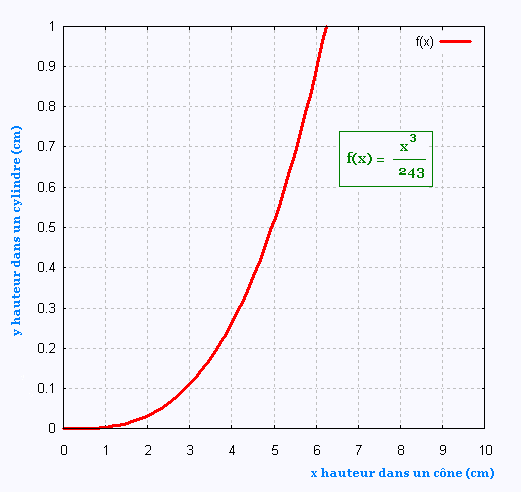
c) Tableu de valeurs de la relation: y = x³/243

x	0	1	2	3	4	5	6	7
y	0.000	0.004	0.033	0.111	0.263	0.514	0.889	1.411

c) Représentation graphique de y en fonction de x: