Mathématiques: Le brevets

Brevet des collèges
Paris, septembre 2002.

Activités numériques

Exercice 1

A = (1/65) - (3/5)÷(12/7)
B = (7 x (10⁵)² x 10^-3)/(35 x 10³)
C = 4√45 + 2√5 - √500

1. A = (1/65) - (3/5) x (7/12) = (1/65) - (7/20) =
(4/260) - (91/260) = - 87/260.

A = - 87/260.

2. B = (7/35) x (10^{10 - 3 - 3}) = (1/5) x 10⁴ =
(10/5) x 10³ = 2.0 x 10³

B = 2.0 x 10³.

3. C = 12√5 + 2√5 - 10√5 = 4√5

C = 4√5.

Exercice 2

D = (2x - 5)(x + 3) - (2x - 5)²

1. D = (2x - 5)(x + 3) - (2x - 5)² =
2x² + 6x - 5x - 15 - (4x² - 20x + 25) =
2x² + 6x - 5x - 15 - 4x² + 20x - 25 =
- 2x² + 21x - 40.

D = - 2x² + 21x - 40.

2. D = (2x - 5)(x + 3) - (2x - 5)² =
(2x - 5)[(x + 3) - (2x - 5)] =
(2x - 5)[x + 3 - 2x + 5] =
(2x - 5)(- x + 8).

D = (2x - 5)(- x + 8).

3. (2x - 5)(- x + 8) = 0 ssi x = 5/2 ou x = 8

x = 5/2 ou x = 8.

Exercice 3

1. 910 pains au chocolat et 693 croissants.

910 = 2 x 5 x 7 x 13
693 = 3² x 7 x 11.

Chaque sachet contient le même nombre de gâteaux.

L'unique facteur commun 7 qui est ici le pgcd(910,693) est le nombre de gateaux dans chaque sachet.

2. Il y a 693/7 = 2 x 5 x 13 = 130 sachets contenants des croissants.

Exercice 4

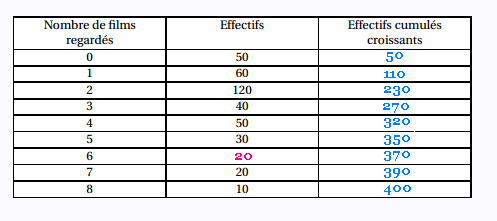
1. Tableau


2. a. Le nombre de personnes qui ont regardé un seul film est égal à 60.

60 personnes.

b. 60/400 = 6/40 = 3/20 1.5/10 = 15%.

15%.

3. Le nombre de personnes qui ont regardé moins de 4 film est égal à 50 + 60 + 120 + 40 = 270 personnes.

270 personnes.

4. En moyenne, le nombre de films que les personnes interrogées ont regardé est la moyenne pondérée de la série condensée:

M = (0 x 50 + 1 x 60 + 2 x 120 + 3 x 40 + 4 x 50 +
5 x 30 + 6 x 20 + 7 x 20 + 8 x 10 )/400 = 1030/400 =
2.575 ≈ 3 (arrondi à l'unité).

Moyenne = 3 films.

Activités gémétriques

Exercice 1

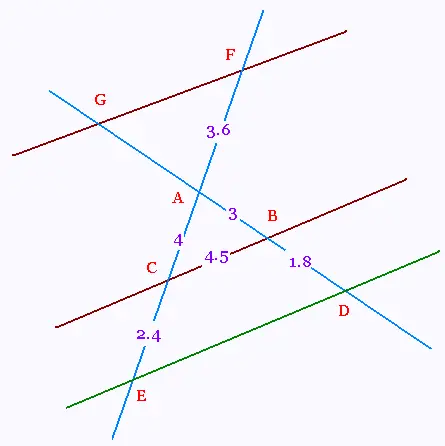
1.
Les droites (BC) et (GF) sont parallèles. Les droites (GB) et (CF) sont sécantes en A. D'après le théorème de Thalès:

AG/AB = AF/AC = GF/BC

AF/AC = GF/BC
3.6/4 = GF/4.5. D'où GF = 4.05 .

GF = 4.05 cm.

2.
AC/AE = 4/6.4 = 10/16 = 5/8

AB/AD = 3/48 = 10/16 = 5/8

D'après the réciproque du théorème de Thalès, les droites (BC) et (ED) sont parallèles.

Exercice 2

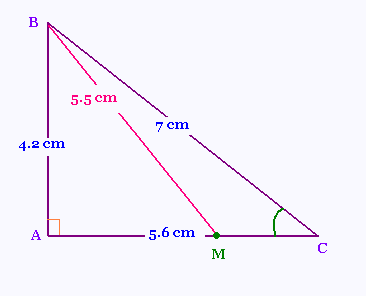
1.
BC² = 7² = 49
AC² + AB² = 4.2² + 5.6² = 17.64 + 31.36 = 49.

BC² = AC² + AB².
D'après la réciproque du théorème de Pythagore, l'angle BAC est droit.

2. tg(∠BCA) = 4.2/5.6 = 0.75

D'où

mes(∠BCA) = tg^-1(0.75) = 36.87 = 37°

mes(∠BCA) = 37°

3. D'après le théorème de Pythagore,

BM² = AM² + AB²

AM² = BM² - AB² =
(5.5)² - 4.2² = 30.25 - 17.64 = 12.61.

AM = √(12.61) = 3.5510 cm = 35 mm.

AM = 35 mm.

Exercice 3

La cloche en forme de demi-sphère de rayon r égal à 9 cm a le même rayon et le même volume qu'un cylindre droit.

Volume (cloche) = (1/2) (4/3) π r³
Volume (cylindre) = π r² x h .

1. Volume (cloche) = (1/2) (4/3) π 9³ =
1526.81 cm³ ≈ 1527 cm³ .

Volume (cloche) = 1527 cm³.

2. On a Volume (cloche) = Volume (cylindre). Donc

(1/2) (4/3) π r³ = π r² x h

D'où

h = (2/3) x r

h = (2/3) x r .

h = (2/3) x r = h = (2/3) x 9 cm = 6 cm.

h = 6 cm.

Problème

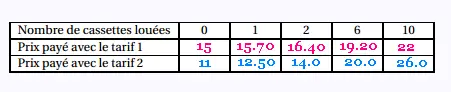
Tarif 1 : Un abonnement mensuel de 15 € et
0,70 € par cassette louée.
Tarif 2 : Un abonnement mensuel de 11 € et
1,50 € par cassette louée.

1.


2. x étant le nombre de cassettes louées par un client en un mois, on a:

a. le prix payé avec le tarif 1, P1(x) = 0,70 x + 15.

b. le prix payé avec le tarif 2, P2(x) = 1,50 x + 11.

3.

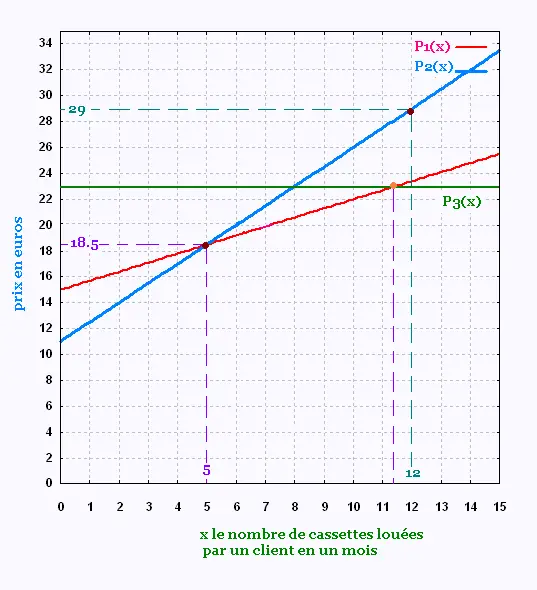
4.
a. Résoudre l’équation 0,7x +15 = 1,5x + 11.
1,5x - 0.7x = 15 - 11
0.8x = 4
x = 4/0.8 = 5

x = 5 .

Pour une location de 5 cassettes, les tarifs 1 et le tarif 2 donnent le même prix.

b. Voir le graph.

5. Au delà de 5 cassettes, le tarif 1 est plus avantageux.

6. Pour 29 €, avec le tarif 2, le graphique donne 12 cassettes.

7.
a. 0,70 x + 15 = 19.90
0,70 x = 19.90 - 15 = 4.90
x = 4.90/0.70 = 7 cassettes.

b. Le prix moyen d'une cassette est 19.90/7 = 2.8428 =
2.84 €.

8.
a. Voir graphique.

b. Au delà de 12 cassettes, le tarif 3 est plus avantageux.