Mathématiques: Le brevets
Brevet des collèges Polynésie juin 2010
Activités numériques
Exercice 1

1. pgcd(120,144) par la méthode de l'algorithme
d'Euclide:
144 = 1 x 120 + 24
120 = 5 x 24 + 0
pgcd(120, 144) = dernier reste non nul = 24.
2. Le nombre de coffrets à préparer est
égal au pgcd(120, 144) = 24.
Chaque coffret doit contenir:
120/24 = 5 flacons de parfum au tiare, et
144/24 = 6 savonnettes au monoï.
3.
a) pgcd(2277, 1449) = dernière différence non nulle = 207.
b) Dans la cellule C2 qui correspond à 208, le résultat
est 2277 - 1449 qui correspond à A2 - B2.
Exercice 2
En tout, nous avons 10 animaux.
Vaite s'assoit au hasard sur le manège du caroussel.
1.
P(Vaite monte sur un cheval) = 4/10 = 2/5.
2.
a
L'événement L est Vaite monte sur un lion.
L'événement non L est Vaite ne monte pas sur un lion.
C'est l'événement complémentaire de l'événement L.
La probabilité de cet événement est égal à 1 - P(Vaite monte sur un lion)
= 1 - 2/10 = 8/10 = 4/5.
b.
Vaite ne peut pas monter à la fois sur deux mêmes animaux en même
temps. Ainsi les événements A et C sont incompatibles.
Par conséquent, la probabilité de l'événement A ou C = P(A ou C) =
P(A) + P(C) = P(âne) + P(coq) = 2/10 + 1/10 = 3/10.
Exercice 3
Il s'agit de calculer les moyennes pondérées
des salaires dans chacune des deux entreprises
et comparer.
La moyenne des salaires dans l'entreprise Hiti est:
Mh = (50 x 168000 + 50 x 120000)/100 =
(168 + 120) x 1000/2 = 288000/2 = 144000 francs.
La moyenne des salaires dans l'entreprise Kalu est:
Mk = (20 x 180000 + 80 x 132000)/100 =
(2 x 180 + 8 x 132) x 100 = 141600 francs.
Mk < Mh. On est donc mieux payé dans l'entreprise Hiti.
Kévin avait tort.
Activités géométriques
Exercice 1
BC = 14 cm, AL = 6 cm et AK = x cm où x
désigne un nombre positif.
Partie 1
BL = 4,8 cm et x = 1 cm.
1. Figure en vraie grandeur.
2. L’aire du triangle BLA = (AL x BL)/2 =
(6 x 4.8)/2 = 14.4 cm2.
3.
Le quadrilatère EFGH est un rectangle. La
propriété Si un quadrilatère est un rectangle alors ses côtés
opposés sont parallèles deux à deux; permet de
conclure que les droites (HG) et (BC) sont parallèles.
4.
Les droites (HG) et (BC) sont parallèles. Les droites (AB)
et (AL) sont sécantes en A.
D’après le théorème de Thalès, on a :
AH/AB = AK/AL = HK/BL
d'où:
HK = BL x AK/AL = 4.8 x 1/6 = 0.8 cm.
Partie 2
BL et x ne sont pas connus.
1. KL = AL - AK = AL - x = 6 - x cm
2.
a.
D'après le tableau, pour x égal à 4,5 cm:
KL = 1.5 cm.
HG = 10.5 cm.
b.
D'après le tableau, l’égalité KL = HG = 4.2
correspond à x = 1.8.
Dans ce cas, le quadrilatère EFGH est un carré.
Exercice 2
1B
2D
3C
Problèmes
Partie A
Une traversée inter-îles de 17 kilomètres.
1. Le premier départ de CatamaranExpress est à
5 h 45 min pour une arrivée à 6 h 15 min.
La durée est donc: 6 h15 mn - 5h 45 mn =
5 h 75 mn - 5h 45 mn = 30 mn.
Sa vitesse moyenne = 17 km/30 mn =
17 km/0.5 = 34 km/h.
2.
La vitesse moyenne de FerryVogue est de 20 km/h.
s’il quitle le quai à 6 h, la durée du trajet sera:
(17/20) h + 6h = 6.85 h = 0.85 x 60 mn = 51 mn.
L'heure prévue de son arrivée est à 6 h 51 mn.
Partie B
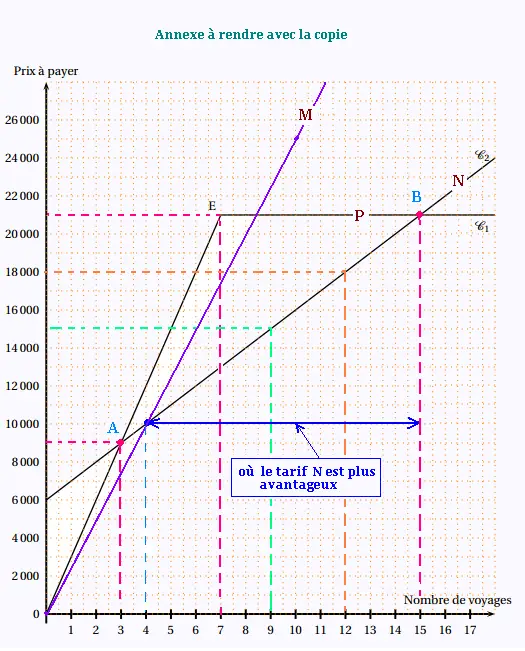
1. Les coordonnées du point E sont:
abscisse = 7 et ordonnée = 21000
2.
Les abscisses des deux points d’intersection des
deux représentations graphiques sont:
3, et 15,
3. La représentations C2 est celle de la fonction g.
g est la seule fonction affine parmis les trois fonctions
représentées. Sa courbe est une droite
ne passant pas par l'origine.
On le vérifie, par exemple pour x = 0 et x = 15.
4.
La lecture sur le graphe donne l'image de 12 par
la fonction g, g(12) = 18000.
Par le calcul, on a: g(12) = 12 x 1000 + 6000 = 18 000
5.
La lecture sur le graphe donne l’antécédent de
15000 par la fonction g, qui vaut 9.
Par le calcul, on a: 15000 = x . 1000 + 6000 . Donc
x = (15000 - 6000)/1000 = 9.
Partie C
La compagnie de transport maritime propose trois tarifs
pour un voyage quel que soit le bateau choisi :
• Tarif M : on paie 2 500 francs chaque voyage.
• Tarif N : on paie une carte mensuelle à 6 000 francs auquelle
s’ajoute 1 000 francs pour chaque voyage.
• Tarif P : on paie 3 000 francs par voyage jusqu’au septième
voyage puis on fixe le prix égal à celui de ce septième
voyage pour les autres traversées jusqu’à la fin du mois.
1.
La courbe C1 correspond au tarif P.
La courbe C2 correspond au tarif N.
2.
La fonction f défnie par : f : x → 2500x
est une fonction linéaire. Sa courbe est une droite
passant par l’origine.
Deux points suffisent à tracer cette courbe:
par exemple le point (0,0) et le point (10, 25000).
3.
Le tarif N est plus avantageux que les deux autres
pour un nombre de voyages compris entre 4 et 15.
|