Mathématiques: Le brevets

Brevet des collèges
Pondichéry mai 2008.

Activités numériques

Exercice 1

1.1 28 x 10^-3 = 0.028

1.2 √50 = 5√2

1.3 (3/4)² - 1/4 = 5/16

1.4 2/3 -5/6 + 1 = 5/6

1.5 L'équation x/2 = 6/5 a pour solution 12/5.

Exercice 2

1.
A = (x - 1)² + x² + (x + 1)²

a) A = x² - 2x + 1 + x² + x² + 2x + 1 =
3x² + 2.

b) Si A = 1325 alors 3x² + 2 = 1325. D'où

3x² = 1325 - 2 = 1323

x² = 1323/3 = 441 = 21² Donc

x = 21

Les 3 nombres entiers positifs consécutifs
sont x - 1 = 20, x = 21, et x + 1 = 22.

2.
B = 9x² - 64

a) B = (3x - 8)(3x + 8)

b) solutions x = 8/3 et x = - 8/3.

Exercice 3

1.
x + y = 45
3x + 5 y = 163

On utilise la méthode de substitution:
On calcule y dans la première équation et on le
substitue dans la deuxième équation.

3x + 5(45 - x) = 163
3x + 225 - 5x = 163
2x = 225 - 163 = 62
x = 31 , d'ou y = 45 - 31 = 14

x = 31, y = 14

2.
Soient:
x le nombre d'objets de type A, et
y le nombre d'objets de type B

Un objet de type A nécessite 3 kg de bois,
Un objet de type B nécessite 5 kg de bois.

Pour une journée, l'entreprise a utilisé 163 kg de bois pour fabriquer 45 objets.

On a le système suivant:

x + y = 45
3x + 5y = 163

Ainsi l'entreprise a fabriqué 31 objets de type A et 14 objets de type B .

Activités géométriques

Exercice 1

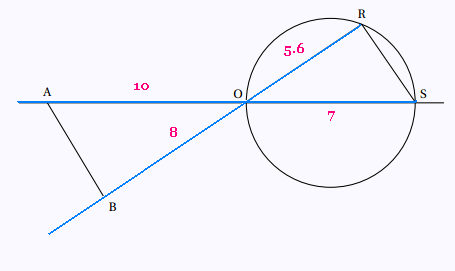On donne: OS = 7 cm, OR = 5.6 cm, OA = 10 cm, et OB = 8 cm

1.
OR/OB = 5.6/8 = 7/10
OS/OA = 7/10

On a donc OR/OB = OS/OA.

D'après le théorème réciproque de Thalès, les droites (AB) et (RS) sont parallèles.

2.
[OS] est le diamètre du cercle. D'après la propriété

Si un triangle est défini par le diamètre d’un cercle et un autre point du cercle, alors ce triangle est rectangle.

le triangle ORS est un triangle rectangle en R.

3.
cos (∠SOR) = 5.6/7 = 0.8
cos^-1(0.8) = 36.87
mes(∠SOR) = 37°

Les angles ∠AOB et ∠SOR sont égaux, puisque ce sont des angles opposés par le sommet.

Donc mes(∠AOB) = mes(∠ SOR)

mes(∠AOB) = 37°.

Problème

Première partie

On répartit 376 cadres et 470 dessous-de-plat dans des colis identiques.

1.
376 = 2 x 188 = 2³ x 47
470 = 2 x 235 = 2 x 5 x 47

pgcd(376, 470) = 2 x 47 = 94

Le nombre maximal de colis réalisables est égal au pgcd(376, 470) = 94.

2.
Dans chaque colis, il y a:

376/94 = 4 cadres et
470/94 = 5 dessous-de-plat.

Deuxième partie

Train 1 : train de marchandises à vitesse constante de 110 km/h quitte Paris à o h 00 mn.

Train 2 : convoi rapide à vitesse constante de 165 km/h quitte Paris à 4 h 00 mn.

1.
a) En 5 heures, le train 1 parcourt la distance de 110 km/h x 5 h = 550 km.

L'origine des distances est Paris, le train 2 quitte Paris à 0 h 00. En i heure, il parcourt 165 km.

b)


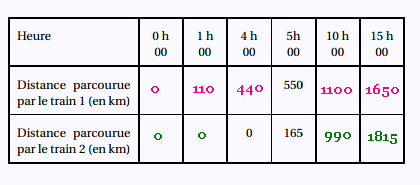
2.
Graphique :



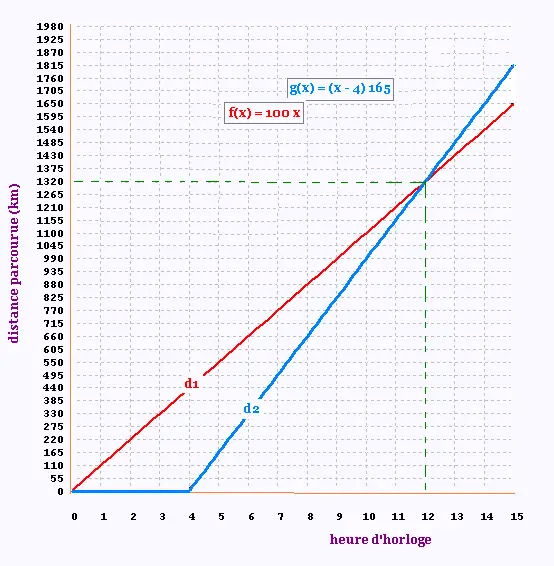
3.
Le train 2 rattrape le train 1 à 12 heures (midi) à 1320 km de Paris.

4.
On souhaite que les colis arrivent le plus tôt possible à leurs destinataires.

a) À Barcelone à 1000 km de Paris, le train 1 est privilégié.

a) À Seville à 1766 km de Paris, le train 2 est privilégié.

Avant midi, à la distance de 1320 km de Paris, le train 1 est en avance sur le train 2. À partir de midi, c'est le train qui dépasse le train 1. De Paris, dès qu'une destination est plus loin que 1320 km, il est avantageux de considérer le train 2.