Mathématiques: Le brevets
Diplôme national du brevet session 2012
Série générale
Activités numériques
Exercice 1
1.
La probabilité qu'Alice gagne une voiture est égale
au (nombre de cas favorables)/(nombre de cas possibles) = 1/3
2.
Avec 4 portes, la probabilité qu'Alice gagne une voiture est égale
au (nombre de cas favorables)/(nombre de cas possibles) = 1/4
1/4 < 1/3 : la probabilité diminue.
Exercice 2
1.
(105 + 1)/105 = 1 + 1/105 =
1 + 1 x 10- 5 = 1 + 0.00001 = 1.00001.
2.
Si avec une calculette on obtient 1, ce résultat affiché
n'est pas exact. Il est tronqué à l'unité ou arrondi à
l'unité.
Antoine a raison.
Exercice 3

Le coureur court 1 kilomètre pour 4 mn 30 sec.
Pour un marathon de 42.195 km. ce coureur, en gardant
la même allure, mettra:
42.195 x (1 mn 30 s) = 42.195 x 4.5 mn = 189.877 mn =
3.1646 h = 3 h + 0.1646 x 60 mn = 3 h 9.8775 mn =
3 h 9 mn + 0.8775 x 60 sec = 5 h 9 mn 53 s.
Le coureur mettra moins de 3 h 30 pour effectuer
le marathon.
Exercice 4
On considère l'équation: (4x - 3)2 - 9 = 0.
1.
Le nombre 3/4 ne vérifie pas cette équation, il
n'est pas une solution de cette équation.
Le nombre 0 vérifie cette équation, il
est donc une solution de cette équation.
2.
(4x - 3)2 - 9 est l'identité
remarquable de la différence des carrés.
(4x - 3)2 - 9 = (4x - 3 + 3)(4x - 3 - 3) =
4x(4x - 6)
3.
Les solutions de cette équation sont x = 0 et
x = 6/4 = 3/2.
Activités géométriques
Exercice 1
1.a.
L'aire du carrée ABCD = 40 cm x 40 cm = 1600 cm2
1.b.
DE = AD - AE = 40 cm - 15 cm = 25 cm
DG = DC + CG = 40 cm + 25 cm = 65 cm.
L'aire du rectangle DEFG = DE x DG = 25 cm x 65 cm = 1625 cm2
2.
En laissant constant la longeur AE = 15 cm
et la longeur CG = 25 cm, on peut trouver
la longeur AB de sorte que l'aire du carré ABCD soit
égale à l'aire du rectangle DEFG.
Il suffit d'ecrire l'égalité des aires:
AB x AD = ED x DG
AD = AB
DG = DC + CG = AB + CG
ED = AB - AE
AB x AB = (AB - AE)(AB + CG)
AB x AB = AB x AB + AB x CG - AE x AB - AE x CG
0 = AB x CG - AE x AB - AE x CG
AB x CG - AE x AB = AE x CG
AB (CG - AE) = AE x CG
AB = AE x CG/(CG - AE)
= 15 x 25/(25 - 15) = 37.5 cm.
AB = 37.5 cm.
Exercice 2
1.
Vcône = π x 22 x 5/3 = 21 cm3
2.
On effectue une section du cône passant par le milieu de
la hauteur et parallèle à la base. On obtient un petit cône.
Cette section a pour rayon x.
The théorème de Thalès permet d'ecrire:
AB/AO = x/2. D'où x = 2 x AB/AO = 2 x 1/2 = 1 cm.
Le rayon du petit cône est donc égal à 1 cm. Sa hauteur
est égal à 2.5 cm.
Le volume du petit cône est égal à:
Vpetit cône = π x 12 x 2.5/3 = 2.6 cm3.
Le volume du petit cône n'est pas égal à la moitié du
volume du cône initial.
Le volume du petit cône est égal au cube de la moitié du
volume du cône initial.
Exercice 3
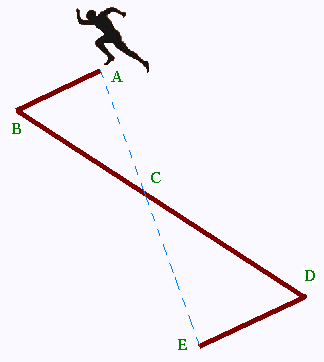
The théorème de Thalès permet d'ecrire:
CA/CE = CB/CD = AB/ED
D'où: CA/CE = AB/ED
CA x ED = CE x AB
ED = CE x AB/CA = 1000 x 300/400 = 750 m
ED = 750 m .
Le théorème de Pythagore permet de calculer les hypoténuses
BC et CD des triangles rectangles ABC et ECD respectivement:
BC2 = AB2 + AC2 =
BC2 = 3002 + 4002 =
(32 + 42) x 1002 = 25 x 1002
= (500)2.
BC = 500 m.
CD2 = CE2 + ED2 =
CD2 = 10002 + 7502 =
(102 + 7.52) x 1002 = 156.25 x 1002
= (1250)2.
CD = 1250 m.
La longeur du parcourt ABCDE est égale à :
AB + BC + CD + DE = 300 + 500 + 1250 + 750 = 2800 m.
La longeur du parcourt ABCDE est égale à 2800 m.
Problèmes
Partie 1
1.
La durée de vol est égale à 10 h 30 - 9 h 35 mn =
9 h 90 mn - 9 h 35 mn = 55 mn.
2.a.
Le nombre de passagers qui ont emprunté le
vol le mercrdi est égal à :
1113 - (152 + 143 + 164 + 189 + 157 + 163) = 145.
2.b.
La moyenne des nombres de passagers par jour cette semaine
est égal à :
1113/7 = 159 passagers par jour.
3.a.
Dans la cellule I2, qui indique 1110, on a saisi le nombre total
des passagers pour la semaine 1. La formule
saisie est =SOMME(B2:H2).
3.b.
Dans la cellule J2, qui indique 159, on a saisi le nombre moyen
de passagers par jour au cours de la semaine 1. La formule
saisie est =MOYENNE(B2:H2).
4.
Le nombre moyen de passagers par jour au cours des
douzes semaines est égal à 166.
L'objectif fixé par la compagnie était un nombre moyen de
passagers par jour supérieur à 80% de la capacité maximale
de l'avion qui est de 190. C'est à dire 80% x 190 = 152
passagers par jour.
166 > 152. Ainsi, la compagnie a atteint son objectif.
Partie 2
1.
Distance Radar-Avion = (300 000 km/s) x (0.0003/2 s) = 90/2 = 45 km.
2.
L'altitude IA de l'avion est donnée par le sinus
de l'angle d'élévation qui est de 5° :
sin 5° = IA/AR. D'où IA = AR x sin 5° = 45 x 0.087 =
3.922008 km = 3922 m.
L'altitude de l'avion à l'instant où il
retourne le signal est de 3922 m.
Partie 3
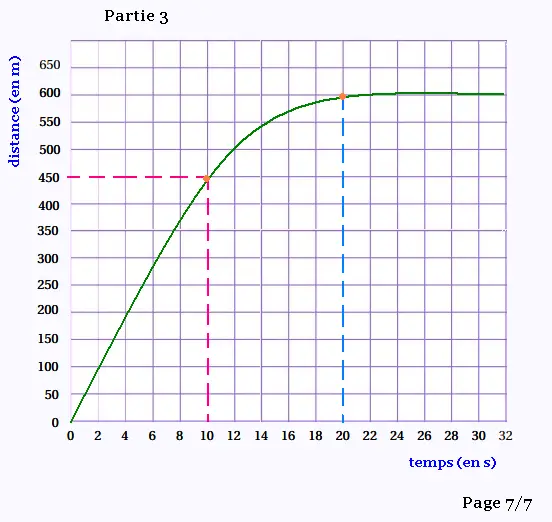
1.
Le graphique donne 450 m pour t = 10 secondes.
L'avion a parcourue 450 m, 10 secondes après avoir
touché le sol.
2.
À 22 secondes, comme à 26 secondes après avoir touché
le sol, l'avion s'est immobilisé. La distance parcourue
devient constante en restant égale à 600 m.
3.
À partir du moment où les roues touche le sol,
l'avion met 20 secones pour s'arrêter.
Au delà des 20 secondes, l'avion reste immobile à la
distance de 600m à partir du point du début de l'attérissage.
|