Mathématiques: Le brevets
Diplôme national du brevet session 2013
Série générale
Exercice 1
Le côté du carré ABCD mesure 4 cm.
La lecture du graphique donne:
1.
Pour l'aire de MNPQ égale à 10 cm2,
AM = 1 cm et AM = 3 cm.
2.
Pour la longeur AM égale à 0.5 cm, l'aire de MNPQ égale
à 12.5 cm2.
3.
L'aire de MNPQ est minimale lorsque AM = 2 cm.
Dans ce cas, elle mesure 8 cm2.
Exercice 2
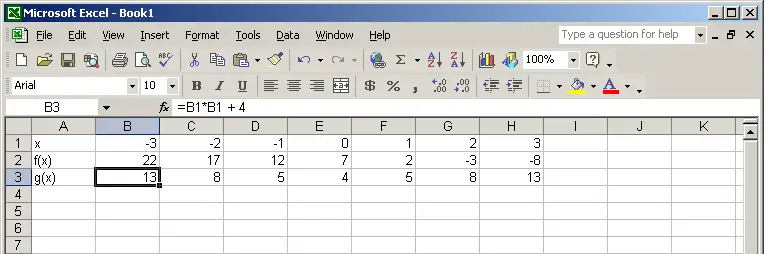
Un tableur, comme excel utilisé ici, donne les images
des valeurs de x par une fonction affine f et par une
fonction quadratique g.
1.
L'image de -3 par f est f(- 3) = 22.
2.
f(7) = - 5 (7) + 7 = - 35 + 7 = - 28.
3.
L'expression de f(x) est :
f(x) = - 5 x + 7
4.
g(x) = x2 + 4. La formule saisie dans la
cellule B3 est = B*B + 4.
Exercice 3
Dans une même entreprise, on compte 10 femmes et
20 hommes.
1.
Salaire moyen des hommes = 1769 €.
Salaire moyen des femmes = (1200 + 1230 + 1250 + 1310 + 1370 + 1400 +
1440 + 1500 + 1700 + 2100)/10 =
1450 €
Le salaire moyen des hommes est plus élevé
que celui des femmes.
2.
On tire au sort une personne de l'entreprise. La
probabilité que ce soit une femme est égale au
nombre de femmes/nombre total des employés = 10/30 = 1/3.
3.
L'étendue est égale à 2400 €. Le plus bas salaire
est 1000 €. Donc le plus haut salaire est égal à
2400 + 1000 = 3400 €.
4.
La médiane est égale à 2000 €. Puisque les salaires
des hommes sont tous différents, on a 50% d'eux qui gagnent
plus de 2000 €. C'est à dire 10 hommes.
Pour les femmes, il y a une seule qui gagne plus de 2000 €.
En tout, dans cette entreprise, il a 11 personnes qui gagnent
plus de 2000 €.
Exercice 4
La figure 1 présente un triangle rectangle en A. La mesure
de l'angle B se calcule par son sinus.
sin (B) = AC/BC = 3/6 = 1/2.
Ainsi B = sin-1(1/2) = 30°.
La figure 2 présente un cercle circonscrit au
triangle ABC. Puisque AB est le diamètre du cercle,
alors ce triangle est rectanle en C.
Puisque mes (A) + mes (B) + mes (C) = 180°, on
a donc
mes (B) = 180°, - mes (A) - mes (C) =
180° - 59° - 90° = 31°.
La figure 3 présente un polygône régulier à 5
côtés, c'est à dire un pentagone.
Selon la propriété:
la somme des mesures des angles intérieurs d'un
polygône de n côtés est égale à (n - 2)180°,
on trouve pour le pentagone (5 - 2)180° =
3 x 180° = 540°.
Puisque le polygône est régulier, donc
mes(B) = 540/5 = 108°.
Exercice 5
1.
Le volume d'un parpaing est égal à 50 cm x 20 cm x 10 cm =
10 000 cm3 = 0.01 m3.
Pour 300 parpaings, le volume est égal à
300 x 0.01 m3 = 3 m3.
Le volume servant de transport du fourgon est égal à
2.6 m x 1.56 m x 1.84 m = 7.46 m3.
On peut donc placer les 300 parpaings dans le fourgon et
faire un seul aller-retour.
Mais la contrainte est dans le poids. La charge pouvant
être transportée est limitée à 1.7 tonnes.
300 parpaings pèsent 300 x 10 kg = 3 000 kg = 3 tonnes.
On doit donc effectuer deux aller-retour. Un aller-retour
avec au plus 170 parpaings et un deuxième avec le reste.
2.
Deux aller-retour comptent 2 x 10 + 2 x 10 km = 40 km.
Le fourgon consomme 8 litres de Diesel aux 100 km. Pour
40 km, Il faut donc (8/100) x 40 = 3.20 litres.
Un litre de carburant coûte 1.50 €. Les deux aller-retour
coûteront donc 3.20 x 1.50 € = 4.8 €.
Le tarif de location du fourgon est pour 1 jour
et 50 km maximum, qui coûte 55 €.
Le coût total du transport est donc
4.8 € + 55 € = 59.8 €.
3.
Le rapport (tarif de location du fourgon)/(distance maximale autorisée par jour)
n'est pas constant. Il décroît : 1.6; 1.1; 0.61; 0.39 . Ainsi
Les tarifs de location du fourgon ne sont pas proportionnels
à la distance maximale autorisée par jour.
Exercice 6
1. a.
On veut déterminer la hauteur du cône de sel OS.
Le diamètre EL du cône est égal à 5 m. Donc EO = 5/2 = 2.5 m.
Les droites (BC) et (OS) sont perpendiculaires à la
droite (AL). Elles sont donc parallèles entre elles.
Les droites (AS) et (AL) sont sécantes en A.
En utilsant le Théorème de Thalès, on a:
AB/AO = BC/OS
OS x AB = AO x BC
D'où OS = AO x BC/AB
AB = 3.20 m
AO = AB + BE + EO = 3.20 + 2.30 + 2.5 = 8 m
BC = 1 m
OS = 8 x 1/3.2 = 2.5 m.
La hauteur du cône de sel est égale à 2.50 mètres.
1. b.
Vcône = π x (rayon)2 x hauteur /3 .
Vcône de sel = π x (2.5)2 x 2.5 /3 = 16.36 m3
≈ 16 cm3.
2.
(rayon)2 = 3 x Vcône/(π x h).
(rayon)2 = 3 x 1000/(π x 6) = 159.15 m2. D'où:
rayon = √159.15 = 12.61 m ≈ 126 dm.
Exercice 7
Affirmation 1
Les 3/4 des adhérents sont mineurs, c'est à dire d'âge
d'au plus 18 ans. Il reste donc 1/4 des adhérents qui
sont majeurs, c'est à dire d'âge d'au moins 18 ans.
Le 1/3 de ces adhérents majeurs a plus de 25 ans. Ainsi
les 2/3 ont entre 18 et 25 ans. C'est à dire (2/3) x (1/4) des
adhérents = 1/6 des adhérents.
L'affirmation proposée est vraie.
Affirmation 2
Si un article est soldé à 30%, alors il
coûte 70% du prix initial.
Si ce 70% du prix initial est suivi d'une autre
baisse de 20%, alors il restera (80%) x (70%) du
prix initial. C'est à dire 56% du prix initial.
Au final, le prix a baissé de 100%- 56% = 44%
L'affirmation proposée est fausse.
Affirmation 3
(n + 1)2 - (n - 1)2 est l'identité
remarquable de la différence des carrés.
(n + 1)2 - (n - 1)2 =
(n + 1 + n - 1)(n + 1 - n + 1) = 2 n x 2 = 4 n.
pour un entier n quelconque.
4 n est un entier qui est toujours un multiple de 4.
L'affirmation proposée est vraie.
|