Mathématiques S:

Échelle logarithmique

Échelle logarithmique

Une échelle est une proportion de taille entre la représentation d’une chose et la chose représentée.

Une échelle est aussi une série de graduations sur un instrument de mesure .

Exemple:

Un thermomètre à alcool comporte souvent une double échelle de mesure: l'échelle Celsius et l'échelle Fahrenheit.

Retenons donc, Une échelle est un système qui permet de graduer une droite d’une certaine manière.

Il existe deux importantes échelles. L'échelle linéaire et l'échelle logarithmique à base 10.

• L' échelle linéaire est une echelle graduée de façon proportionnelle.



La distance b - a = 10 , séparant deux nombres a et b, est constante.

L'échelle linéaire est utilisé lorsque l'écart entre les données à représenter n'est pas large. Exemple l'eéchelle Celsius des températures.


• L' échelle logarithmique est basée sur la fonction log.

L'échelle logarithmique est une alternative à l'échelle linéaire.


Le principe est le suivant :

la distance séparant deux nombres a et b est log(b) – log(a).
La distance séparant 1 et 10 est donc log(10) – log(1).
La distance séparant 10 et 100 est donc log(100) – log(10).

Le rapport b/a = 10 , séparant deux nombres a et b = 10 a , est constant.



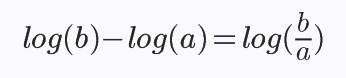
Or 10/1 = 100/10 = 1000/100 :

Ainsi, la distance entre 1 et 10 est la même qu’entre 10 et 100 et entre 1000 et 100.

La distance qui sépare 0.1 de 1 est la même que celle qui sépare 1 de 10 et celle qui sépare 10 de 1000 ou de 100 de 1000; car log(1000) - log(100) = log(100) - log(10) = log(10) - log(1) = log(1) - log(0.1).

Chacun de ces intervalles s'appelle un module .

Les logarithmes des modules ont des longeures égales à 1 . Mais à l'intérieur de chaque module, on insère la même graduation logarithmique basée sur les écarts logarithmiques .




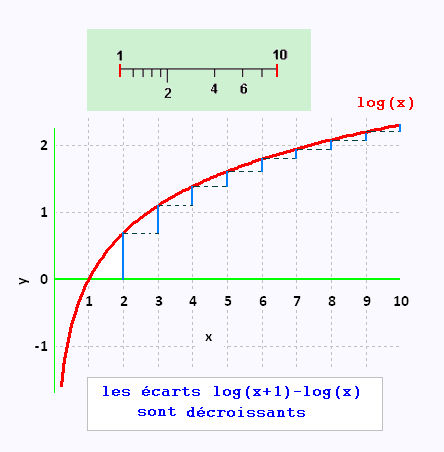
• L'échelle logarithmique n'est définie que pour des valeurs strictement positives.

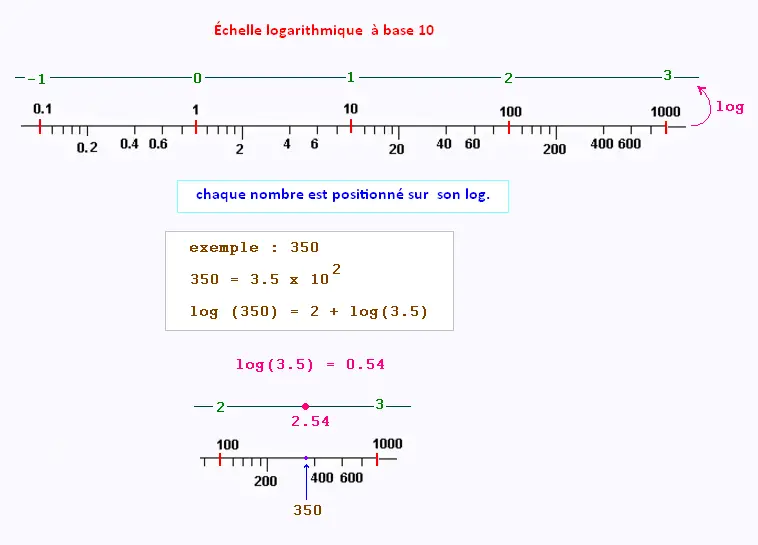
• Dans ce système de graduation, le nombre x est placé à une distance log(x) de l'origine. log(x) est sa coordonnée logarithmique .

• Le logarithme employé ici est le logarithme décimal, c'est à dire à base 10.

Une échelle logarithmique est un système de graduation en progression géométrique. La position d'une valeur sur l'axe, c'est son logarithme.



L'échelle logarithmique est particulièrement adapté pour rendre compte des ordres de grandeur dans les applications.

Lorsqu'on étudie un phénomène utilisant une gamme étendue de valeurs, l'échelle linéaire est mal adaptée. On lui préfère une échelle logarithmique qui espace les valeurs faibles et rapproche les valeurs fortes .

À partir de cette échelle, on construit des des repères log-log ou semi-log.

Un repère semi-logarithmique est un repère dans lequel l'un des axes est gradué selon une échelle linéaire, alors que l'autre axe est gradué selon une échelle logarithmique.

Le repère semi-logarithmique permet de représenter des phénomènes exponentiels.