Mathématiques 45: Géométrie:
Triangles isométriques
Triangles semblables
Cas d'isométrie des triangles
Cas de similitude des triangles

1. Cas d'isométrie (congruence) des triangles

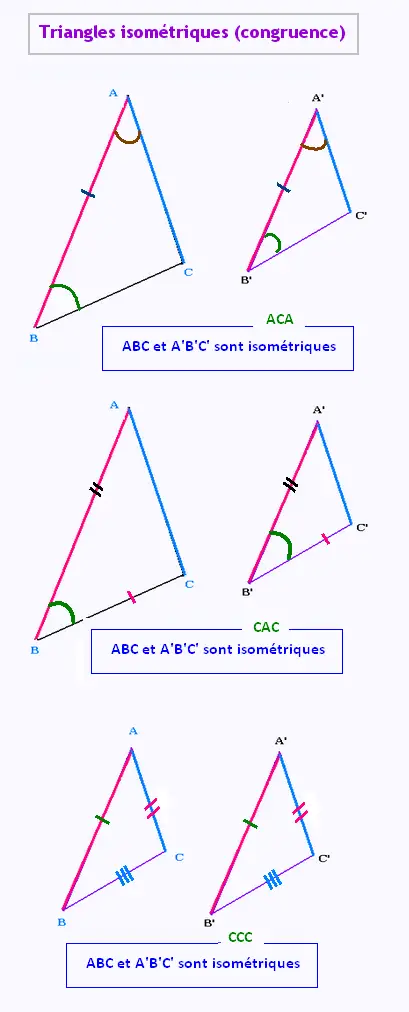
Lorsque deux triangles sont parfaitement identiques (mêmes côtés et mêmes angles), on dit qu’ils sont congrus (ou isométriques).

On utilise le symbole ≅ pour signifier la congruence.

On appelle conditions minimales (ou cas de congruence) les caractéristiques minimales permettant pour affirmer que deux triangles sont isométriques.

Il existe trois cas de congruence pour les triangles:

CCC (Côté-Côté-Côté)
CAC (Côté-Angle-Côté)
ACA (Angle-Côté-Angle)

2. Cas de similitude des triangles

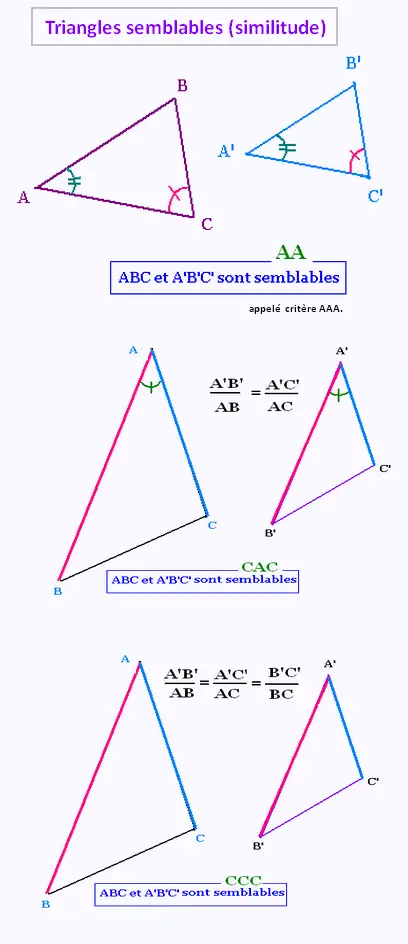
Deux triangles qui ont les mêmes angles et des rapports de côtés homologues proportionnels sont dits semblables.

Cela signifie qu'ils sont similaires. Ils ont la même forme, mais pas nécessairement la même grandeur. L'un est une réduction ou un agrandissement de l'autre.

On utilise le symbole ∼ pour signifier la similitude.

On appelle conditions minimales (ou cas de similitude) les caractéristiques minimales permettant d'affirmer que deux triangles sont semblables.

Il existe trois cas de similitude pour les triangles:

CCC (Côté-Côté-Côté)
CAC (Côté-Angle-Côté)
AA (Côté-Angle-Angle)