Mathématiques 2: Similitude
1. Rapport de similitude K
1.Le rapport de similitude K est le rapport entre les mesures de longueurs des segments homologues .
2. Le rapport entre les périmètres semblables
est égal au rapport de similitude K.
3. Le rapport entre les aires semblables est égal au
carré du rapport de similitude K2.
4. Le rapport entre les volumes semblables est égal au
cube du rapport de similitude K3.
5. Deux figures sont équivalentes si elles ont la même aire.
2. Exemples
2.1. Exemple 1
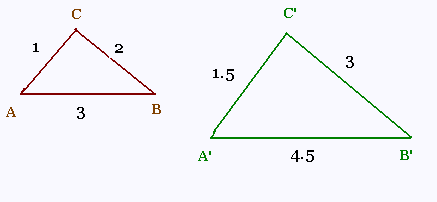
Les triangles ABC et A'B'C' sont semblables :
Le rapport de similitude s'ecrit:
K = A'B'/AB = 4.5/3 = 1.5
K = A'C'/AC = 1.5/1 = 1.5
K = B'C'/BC = 3/2 = 1.5
K = perimètre (A'B'C')/périmètre (ABC) = (4.5 + 1.5 + 3)/(1 + 2 + 3) = 9/6 = 1.5
2.2. Exemple 2
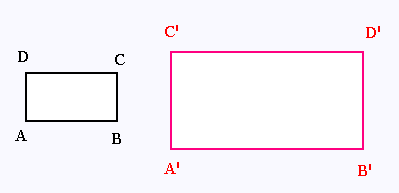
L'aire du premier rectangle ABCD est égale à 50 cm2,
celle du deuxième rectangle A'B'C'D' est égale à 200 cm2.
Le rapport des aires K2 est égal à
K2 = 200/50 = 4
Donc K = √4 = 2
2.3. Exemple 3
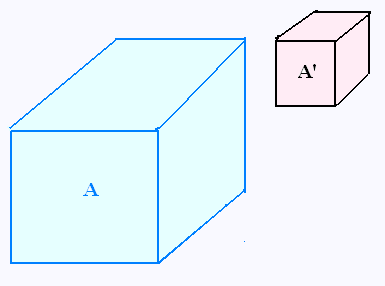
Le volume du prisme A est égale à 64 cm3,
celui du deuxième prisme A' est égale à 8 cm3.
Le rapport des volumes K3 est égal à
K3 = 64/ 8 = 8
Donc K = 2
3. Résumé
Si K2 = rapport des aires , alors
K = rapport des côtés homologues.
Si K3 = rapport des volumes , alors
K = rapport des côtés homologues.
Les côtés homologues sont les côtés qui se correspondent.
Par exemple, les rayons entre eux, les hauteures
entre elles, les apothèmes entre eux, les arcs entre eux, les longeurs entre elles, les largeures entre elles, etc ...
4. Exercices
4.1. Exercice 1: disque
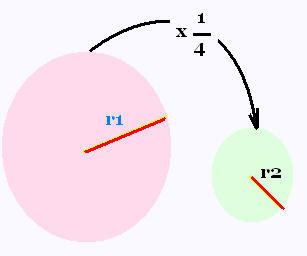 La surface d'un grand disque de rayon r1 = 10 cm est transformée par une réduction au quart en une deuxième surface d'un petit disque. Quel est le rayon r2 de ce dernier?
La surface d'un grand disque de rayon r1 = 10 cm est transformée par une réduction au quart en une deuxième surface d'un petit disque. Quel est le rayon r2 de ce dernier?
Réponse::
L'air du premier disque est égale à πr12
L'air du deuxième disque est égale à πr22
Le rapport des aires des surfaces est égal à K2 = πr22/πr12 = r22/r12 =
(r2/r1)2
Donc K = r2/r1
Le rapport des aires est égal à K2 = 1/4
Donc K = √(1/4) = 1/2 = 0.5
Ainsi K = 0.5 = r2 /r1 donc r2 = 0.5 x r1 = 0.5 x 10 =
5 cm.
4.2. Exercice 2: cylindre
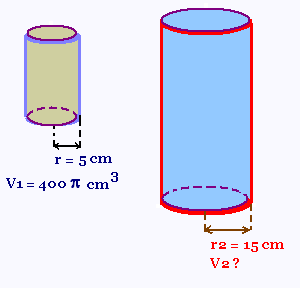 Le volume V1 d'un petit cylindre de rayon de base = 5 cm
est de 400π cm3. Quel est le volume V2
d'un grand cylindre de rayon de base 15, cm qui serait semblable
au premier?
Le volume V1 d'un petit cylindre de rayon de base = 5 cm
est de 400π cm3. Quel est le volume V2
d'un grand cylindre de rayon de base 15, cm qui serait semblable
au premier?
K = 15 cm/5 cm = 3
Donc K3 = 33 = 27
K3 = V2/V1 = V2/400π
Ainsi V2 = 27 x 400π = 10800 π cm3 = 34.0 dm3.
4.3. Exercice 3: prisme à base rectangulaire
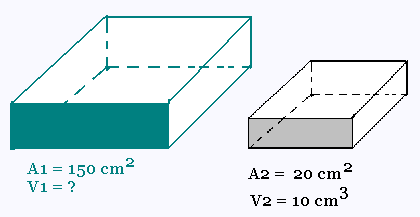
L'aire de base d'un grand prisme à base rectangulaire
est de 150 cm2. Pour un deuxième
petit prisme à base rectangulaire semblable, son aire de base est de 20 cm2, et son volume est de 10 cm3.
Quel est le volume du premier prisme?
K 2 = 20/150
Donc K = ...
Ainsi K3 = 0.005
K3 = V2/V1
V1 = 205.40 cm3.
4.4. Exercice 4: prisme à base triangulaire
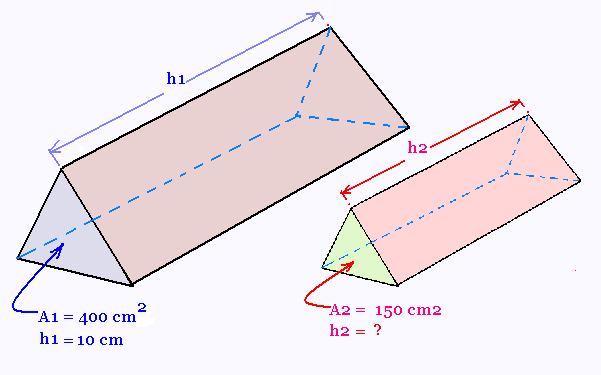
L'aire de base d'un grand prisme à base triangulaire
est de 400 cm2. Sa hauteur h1 est de 10 cm. Pour un deuxième petit prisme à base triangulaire semblable, son aire de base est de 150 cm2.
Quel est la hauteur h2 de ce dernier prisme?
K 2 = 150/400
Donc K = ...
K = h2/h1
Ainsi
h2 = 6.12 cm.
|