Mathématiques 45: Géométrie:
Les coniques: Le cercle
1. Définition du cercle
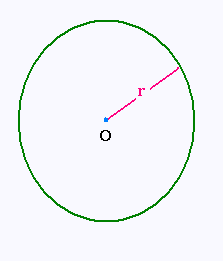
Un cercle est un lieu géométrique. Tous
les points sur le cercle sont à même distance r, appelé rayon, d’un point fixe O
appelé centre du cercle.
2. Équation du cercle
2.1. Equation du cercle: forme générale
la forme générale de l'équation d'un cercle
est:
Ax2 + By2 + Cx + Dy + E = 0
A, B, C, D et E sont des constantes.
2.2. Equation du cercle: forme canonique
la forme canonique de l'équation d'une cercle
est:
(x - h)2 + (y - k)2 = r2
(h, k) sont les coordonnées du centre du cercle.
3. Exemples
3.1. Exemple 1: Cercle centré à l’origine
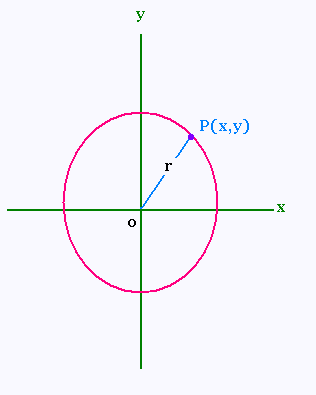
La formule de la distance entre deux points, ou le théorème de Pythagore, nous donne cette équation.
d(P, O) = r =
√[(x - 0)2 + ( y - 0)2]
Ainsi:
x2 + y2 = r2
x2 + y2 - r2 = 0
est l'équation sous forme générale d'un cercle de rayon r sur un plan cartésien.
(x - 0)2 + (y - 0)2 = r2
est l'équation sous forme canonique d'un cercle de rayon r sur un plan cartésien.
3.2. Exemple 2: Cercle centré au point (h,k)
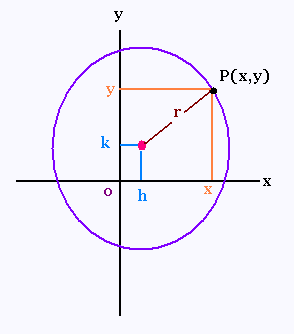
Le centre du cercle a pour coordonnées
h et k.
La formule de la distance entre deux points, ou le théorème de Pythagore, nous donne cette équation.
d(P, O) = r =
√[(x - h)2 + (y - k)2]
Ainsi:
(x - h)2 + (y - k)2 = r2
(x - h)2 + (y - k)2 = r2
C'est l'équation sous forme caconique d'un cercle de rayon r sur un plan cartésien.
Pour obtenir la forme générale, il suffit de décomposer la
forme canoique et obtenir une expression de la forme:
Ax2 + By2 + Cx + Dy + E = 0
3.3. Exemple 3
Quelle est l’équation sous sa forme générale,
de l'équation d'un cercle donnée sous sa forme
canonique suivante:
(x - 2)2 + (y + 3)2 = 49
x2 - 4x + 4 + y2 + 6y + 9 = 49
x2 + y2 - 4x + 6y = 36
x2 + y2 - 4x + 6y - 36 = 0
est l'équation cherchée.
3.4. Exemple 4
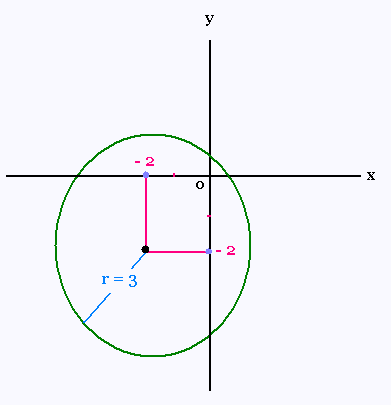
a) Quelle est l’équation, sous sa forme canonique,
du cercle illustré ci-contre?
h = - 2 , k = - 2 et r = 3
La forme canonique de l'équation du cercle
est :
(x + 2)2 + (y + 2)2 = 9
Sa forme générale est:
x2 + 4x + 4 + y2 +
4y + 4 = 9
ou
x2 + y2 + 4x + 4y - 1 = 0
3.5. Exemple 5
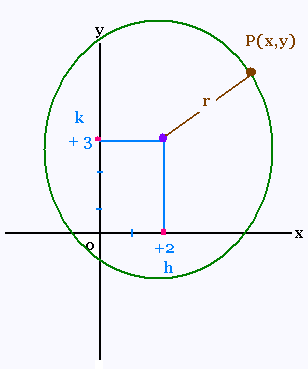
Quelle est l’équation sous sa forme canonique,
de l'équation d'un cercle donnée sous sa forme
générale suivante:
x2 + y2 - 4x - 6y - 3 = 0
Il suffit de factoriser.
x2 + y2 - 4x - 6y - 3 =
x2 - 4x + 4 - 4 + y2 - 6y
+9 - 9 - 3 =
x2 - 4x + 4 + y2 - 6y +
9 - 4 - 9 - 3 =
(x - 2)2 + (y - 3)2 - 16
Ainsi, la forme canonique s'ecrit:
(x - 2)2 + (y - 3)2 = 16
(x - 2)2 + (y - 3)2 = 42
3.6. Exemple 6
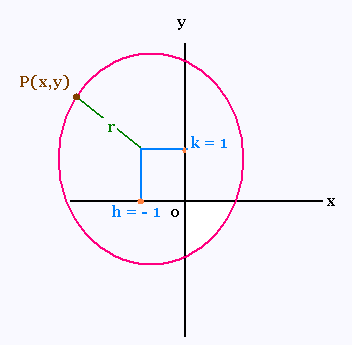
Exprimer l’équation suivante sous sa forme canonique.
3x2 + 3y2 + 6x - 6y - 21 = 0
Simplifier l'équation en divisant par 3:
x2 + y2 + 2x - 2y - 7 = 0
x2 + 2x + 1 - 1 + y2
- 2y + 1 - 1 - 7 = 0
x2 + 2x + 1 + y2
- 2y + 1 - 1 - 1 - 7 = 0
(x + 1)2 + (y - 1)2
- 9 = 0
L'équation cherchée est:
(x + 1)2 + (y - 1)2 = 32
|