Mathématiques 45: Géométrie:
Les coniques: L’hyperbole

1. Définition de l'hyperbole

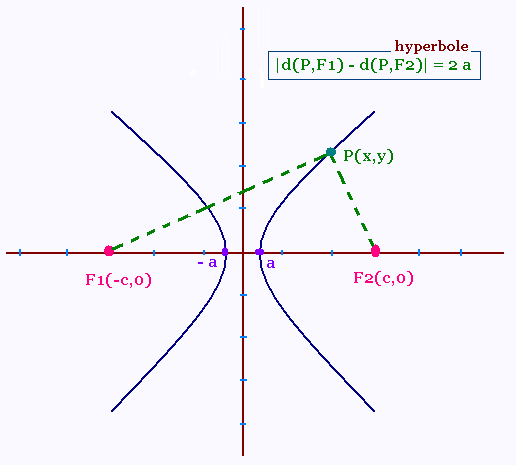
Une hyperbole est un lieu géométrique. Tous les points sur l'hyperbole sont à même valeur absolue de la différence de deux distances de deux points fixes sur l'axe appelés foyers de l'hyperbole.

|d(P, F1) - d(P, F2)| = Constante.

2. Propriétés de l'hyperbole centrée à l'origine

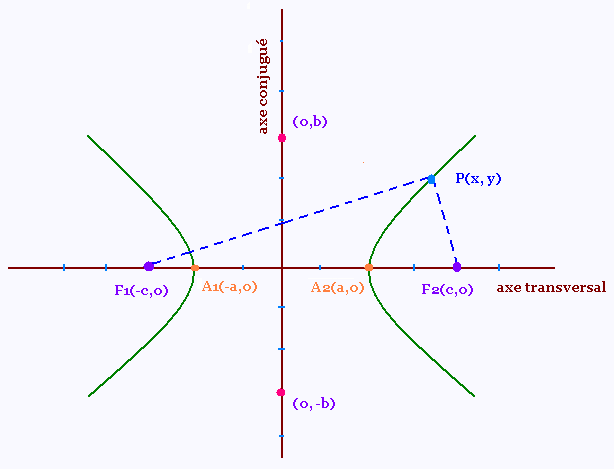
Le centre de l’hyperbole est le point milieu du segment joignant les deux foyers F1 et F2.

L'axe transversal est la droite qui passe par les foyers.

L'axe conjugué est la droite perpendiculaire à l’axe transversal passant par le centre de l'hyperbole.

Les sommet sont les points A1(- a, 0) et A2 (+ a, 0). Ce sont chacune des intersections de l’hyperbole avec ses axes.

Le grand axe est le segment de l’axe transversal qui relie les deux sommets.

Le petit axe est le segment de l’axe conjugué qui relie les deux sommets.

1. Si les foyers sont sur l’axe des x:

F1 (- c, 0) et F2 (+ c, 0).

|d(P,F1) - d(P,F2)| = 2a

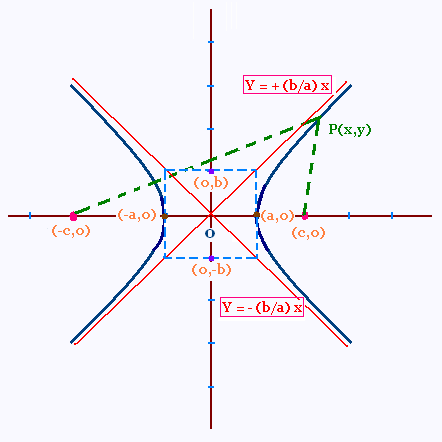
c² = a² + b²

Équation des deux asymptotes :

Y = ± (b/a) x

Les asymptotes touchent les 4 sommets du rectangle (a,b).

2. Si les foyers sont sur l’axe des y:

F1 (0, - c) et F2 (0, +c).

|d(P, F1) - d(P, F2)| = 2b

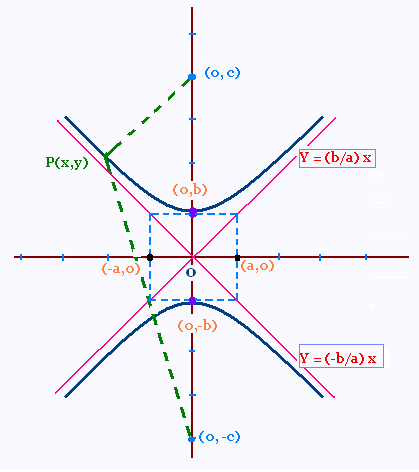
c² = b² + a²

Équation des deux asymptotes :

Y = ± (b/a) x

Les asymptotes touchent les 4 sommets du rectangle (a,b).

La mesure du grand axe
est toujours égale à la
somme des distances aux
foyers.

3. Équation de l'hyperbole centrée à l'origine

L’équation d’une hyperbole centrée à l’origine dépend de l’orientation de l’axe transversal.

1 - Axe transversal horizontal

Sous la forme canonique : x²/a² - y²/b² = 1

Sous la forme générale : Ax² + By² + C = 0

A est une constante positives,
et B et C sont des constante négative

2 - Axe transversal vertical

Sous la forme canonique : y²/b² - x²/a² = 1

Sous la forme générale : Ax² + By² + C = 0

B est une constante positives,
et A et C sont des constante négative

4. Exemples

4.1. Exemple 1:

Donner l’équation de cette hyperbole:

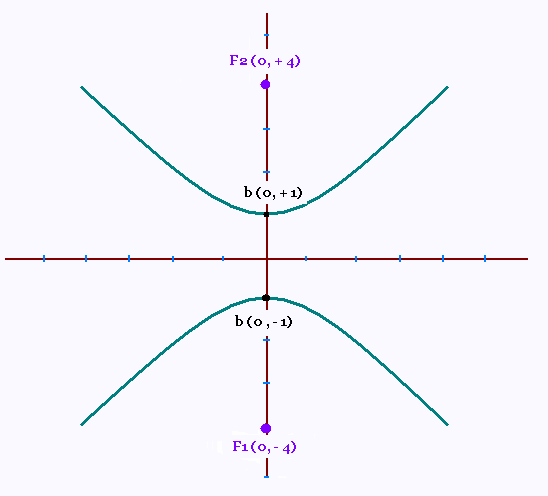
On connait b et c, calculons a: a² = c² - b²

a² = 4² - 1² = 15.

L’équation canonique de cette hyperbole est donc:

y²/1 - x²/15 = 1

Sous forme générale, on a:

- x² + 15y² - 15 = 0