Maths
- 45 -
Les coniques
Applications
© The scientific sentence. 2013
|
Mathématiques 45: Géométrie:
Les coniques: : La parabole
1. Définition de la parabole
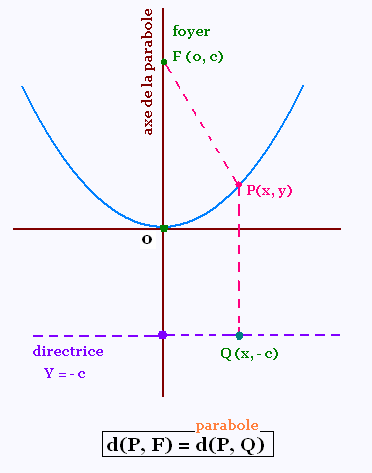
Une parabole est un lieu géométrique.
Tous les points sur la parabole sont à même distance d'un point fixe appelé foyer de la parabole et d’une droite fixe, appelée directrice.
d(P, F) = d(P, Q) = Constante.
Le sommet de la parabole est le point milieu entre son foyer et le point de la directrice intersectant l’axe de la parabole.
La directrice d'une parabole est une droite perpendiculaire à l'axe de la parabole.
L'axe de la parabole est l'axe de symétrie de la parabole.
La distance de valeur égale à c, entre le sommet O(0, 0) et le foyer F(0, c) s'appelle distance focale.
Exemple
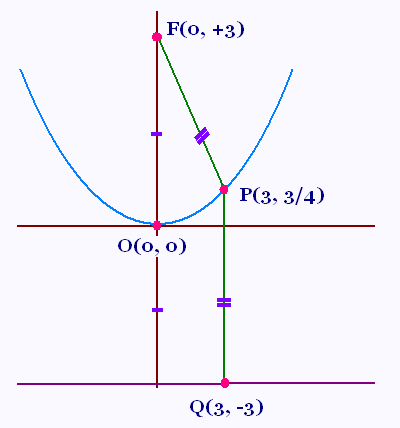
Les distances entre les deux points P(3, 3/4) sur la parabole et Q(3, - 3) sur la directrice et le foyer de la parabole F(0, + 3) sont:
d(P, F) = √[(0 - 3)2 + (3 - 3/4)2] =
√[ 32 + (9/4)2] =
√[ 9 + (9/4)2] =
15/4.
d(P, Q) = √[(3 - 3)2 + (- 3 - 3/4)2] =
√[(- 15/4)2] = 15/4.
2. Équation de la parabole centrée à l'origine
L'équation générale d'une parabole est
de la forme:
Axe vertical: x2 = 4cy
Axe horizontal: y2 = 4cx
c est une constante.
☛ La position du foyer, c'est à dire la valeur de c, se mesure à partir
du sommet.
Nous avons quatre cas possibles:
L'axe de la parabole est vertical
c > 0 : x2 = 4cy
c < 0 : x2 = 4cy
L'axe de la parabole est horizontal
c > 0 : y2 = 4cx
c < 0 : y2 = 4cx
Exemple
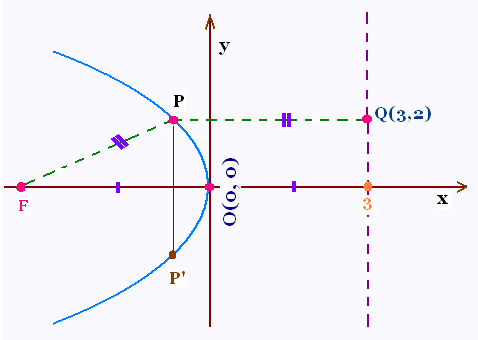
Quelle est l'équation de cette parabole?
La directrice X = 3 donne la valeur
de c du foyer F .
c = - 3
L'équation de la parabole est
donc:
y2 = 4 c x = 4 (-3) x
= - 12 x
Si l'abscisse du point P est - 1/3, alors
son ordonnée est:
y = √ [- 12 x (- 1/3)] = ± 2.
3. Équation de l'parabole centrée au point(h, k)
3.1. Axe vertical
Foyer (h, c + k)
Directrice : y = - c + k
l'équation d'une parabole
centrée au point(h, k) est:
(x - h)2 = 4c(y - k)
Exemple :
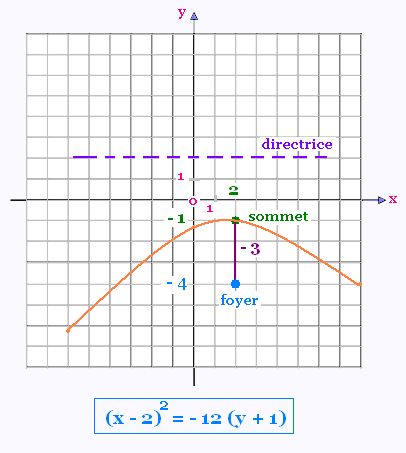
L'équation:
(x - 2)2 = - 12(y + 1)
est une parabole d'axe vertical.
Son sommet est le point (h, k) = (2, - 1)
On calcule c:
- 12 = 4c . D'où c = - 3
Le foyer de la parabole est le point
(h, c + k) = (2, - 3 - 1) = (2, - 4)
La directrice de la parabole est la droite d'équation :
y = - c + k = 3 - 1 = + 2.
3.2. Axe horizontal
Foyer (c + h, k)
Directrice : x = - c + h
l'équation d'une parabole centrée au point(h, k) est:
(y - k)2 = 4c(x – h)
Exemple :
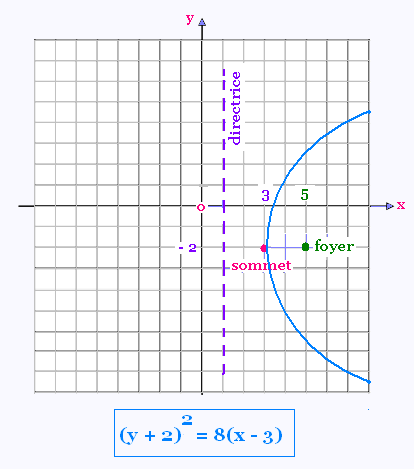
L'équation:
(y + 2)2 = 8(x - 3)
est une parabole d'axe horizontal.
Son sommet est le point (h, k) = (3, - 2)
On calcule c:
8 = 4c . D'où c = + 2
Le foyer de la parabole est le point
(c + h, k) = (2 + 3, - 2) = (5, - 2)
La directrice de la parabole est la droite d'équation :
Directrice : x = - 2 + 3 = + 1
|
|