Maths
- 2 -
Tests
de connaissances
© The scientific sentence. 2010
| Mathématiques 2: Angles et polygones
Exercice 1
1.1. Angles
Compléter:
Un angle est défini par l'.... de deux demi-droites.
Le point d'intersection s'appelle le ..... de l'angle et
les demi-droites, les côtés de l'angle.
Un angle est représenté par son sommet ou à l'aide
de ses côtés .
Un angle aigu mesure moins que 90°.
Un angle obtus mesure plus que 90°.
Un angle ... mesure 90°.
L'angle nul mesure 0°.
L'angle ... mesure 180°.
L'angle plein mesure 360°.
La bissectrice d'un angle est la droite qui passane par
le .... de l'angle et qui partage cet angle en deux
angles de même mesure.
Deux angles ayant un même sommet
et un côté commun sont .... .
Deux angles sont complémentaires si la somme de
leurs mesuresest égale à .... ° .
Deux angles sont supplémentaires si la somme de
leurs mesures est égale à 180° .
La somme des mesures des ..... ......
d’un triangle vaut 180°
La somme des mesures des angles intérieurs
d’un ..... vaut 360°.
La somme des mesures des angles intérieurs
d’un polygone de N côtés vaut (N - 2) x 180°.
Les angles opposés par le sommet sont .... .
Il sont construits par deux droites sécantes.
Les angles correspondants et les angles
alternes-internes sont construits par deux
droites et une sécante.
Si ces deux droites sont parallèles, alors:
Les angles correspondants sont .... .
Les angles ...-... sont égaux.
Si les angles alternes-internes sont égaux
alors leurs droites sont parallèles.
Si les angles correspondants sont égaux
alors leurs droites sont parallèles.
1.2. Triangles
Compléter:
Un triangle est formé de trois côtés.
Un triangle isocèle est un triangle
qui a .... côtés de même mesure.
Un triangle équilatéral a ses trois côtés de même .....
Si un triangle est isocèle alors ses angles
à la base sont ....
Dans un triangle équilatéral, tous les angles sont égaux à 60°.
Inégalité triangulaire : dans un triangle, la somme des
longueurs des deux plus petits côtés est ..... ou
égale à la mesure du plus grand côté.
La hauteur d'un triangle est la droite (ou segment
de droite) issu d'un somet et ...... au côté qui
lui est opposé.
Dans un triangle les hauteurs sont concourantes en
L'.... du triangle est le point de rencontre
de ses hauteurs.
Dans un triangle la ..... est le segment
joignant un sommet au milieu du côté opposé.
Dans un triangle, les médianes sont concourantes en un
point appelé le centre de .... ... .......
Dans un triangle, les bissectrices sont concourantes
au centre du cercle ..... au triangle.
Le cercle inscrit au triangle est le cercle
tangent aux 3 côtés du triangle.
Dans un triangle, les ..... des trois côtés sont
concourantes au centre du cercle circonscrit au triangle.
Le cercle circonscrit est le cercle qui passe par
tous les sommets.
Dans un triangle .... en un sommet, la hauteur,
la bissectrice, la médiane issue de ce sommet, et
la médiatrice de son côté opposé sont confondues.
Si un triangle a ses angles à la base égaux alors
il est .... .
Si dans un triangle la .... issue d'un sommet
et la médiatrice de sont côté opposé sont confondues
alors il est isocèle en ce sommet.
Si dans un triangle la .... issue d'un
sommet et la bissectrice de ce sommet sont confondues
alors il est isocèle en ce sommet.
Si dans un triangle la médiane et la hauteur issues
d'un sommet sont .... alors il est isocèle en
ce sommet.
Si dans un triangle la hauteur issue d'un sommet et la
médiatrice de son côté opposé sont confondues alors il
est .... en ce sommet.
Si dans un triangle la hauteur issue d'un sommet et
la bissectrice de ce sommet sont confondues alors il
est .... en ce sommet.
Si dans un triangle la bissectrice d'un sommet et la
médiatrice de son côté opposé sont confondues
alors il est .... en ce sommet.
Dans un triangle équilatéral, les hauteurs, .....,
médiatrices, bissectrices sont confondues.
Si un triangle a tous ses trois angles égaux (à 60°),
alors il est ...... .
Si dans un triangle, toutes les hauteurs, médianes, médiatrices, et
bissectrices sont confondues alors il est ..... .
Un triangle rectangle est un triangle qui a
deux côtés ..... .
Le côté opposé au sommet de l’angle droit s’appelle l’... du triangle rectangle.
Le centre du cercle .... à un triangle rectangle est
le milieu de l'hypoténuse.
Si un triangle est rectangle, alors le milieu de l’.... est le centre du cercle circonscrit au triangle.
Si un triangle est rectangle, alors le milieu de son hypoténuse est à égale distance des trois ..... .
Théorème de la médiane
Le segment-médiane issu du sommet de l’angle droit a pour longueur la .... de la longueur de l’hypoténuse.
Si un triangle est inscrit dans un cercle de diamètre un des côtés du triangle, alors ce .... est rectangle.
Si on joint un point d'un cercle aux extrémités d'un
diamètre, alors on obtient un triangle rectangle d'hypoténuse égale au .... de ce cercle.
Dans un triangle, si le ..... d’un côté est à égale distance des trois sommets, alors ce triangle est rectangle
Dans un triangle, si le milieu d’un côté est le centre du
cercle .... au triangle, alors ce triangle est
rectangle.
Exercice 2
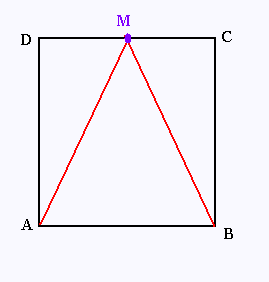
Le quadrilatère ABCD est un carré.
M est le milieu du côté DC.
Question:
Montrer que le triangle AMB est isocèle.
Exercice 3
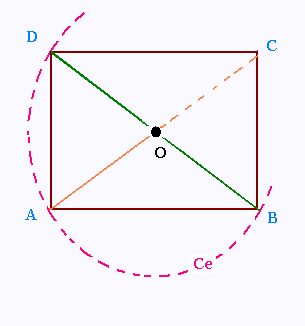
ABCD est un rectangle.
Question:
Montrer que le point O, d'intersection des diagonales
du rectangle, est aussi le point d'intersection des
médiatrices du triangle ABD.
Exercice 4
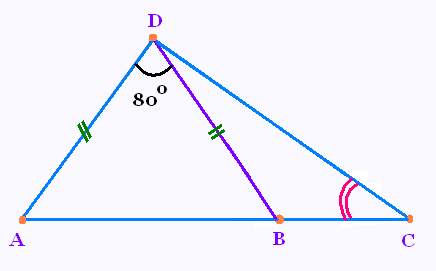
Question:
ABD est isocèle en D.
mes(ADB) = 80°.
L'angle ACD est la moitié de l'angle ADB.
Démontrer que l'angle ADC est droit.
Exercice 5
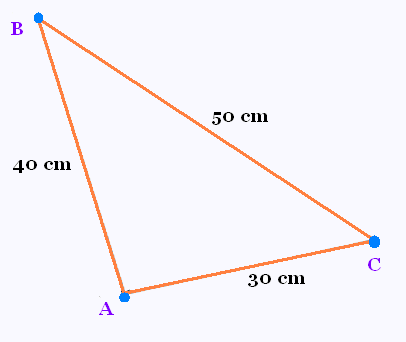
Question:
Démontrer que le triangle ABC doit être un triangle rectangle.
Exercice 6
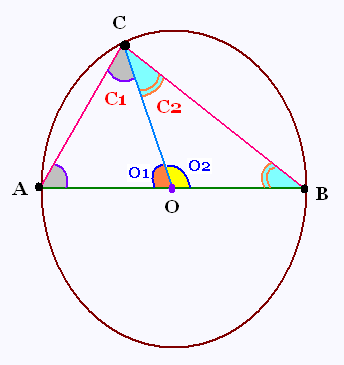
Question:
Montrer que l'angle C est droit.
Exercice 7 : Rectangle d'or
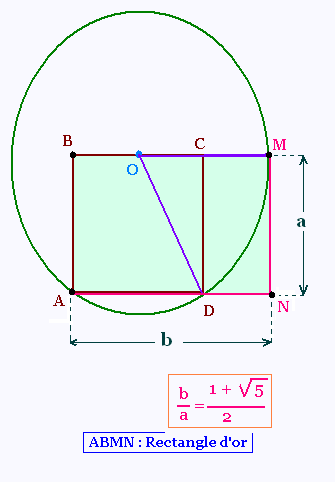
Questions:
a) Constructruire un rectangle d'or :
- Tracer un carré ABCD,
- Noter O le milieu de [BC],
- Tracer un cercle C de centre O et de rayon (OD),
- Prolonger [OC) jusqu'au cercle,
- Noter M le point d'intersection de (OC) sur ce cercle,
- Prolonger [AD],
- Dresser la perpendiculaire à partir du point M,
sur ce prolongement de [AD],
- Noter N le point d'intersection.
Le rectangle obtenu ABMN est un rectangle d'or.
b) Montrer que b/a = (1 + √5)/2.
Exercice 8
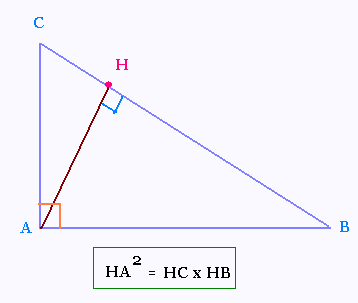
ABC est un triangle rectangle.
[AH] est la hauteur sur [BC] issue du sommet A.
Questions:
Montrer que:
HA2 = HC2 + HB2
.
Exercice 9
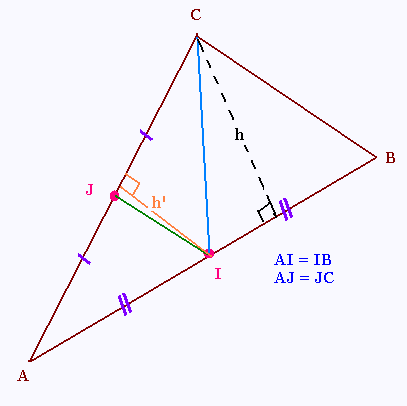
ABC est un triangle .
I est le milieu du côté AB et J le milieu du côté
de AC.
Montrer que:
a)Aire AIC = Aire ABC/2
b)Aire AIJ = Aire AIC/2
.
Exercice 10
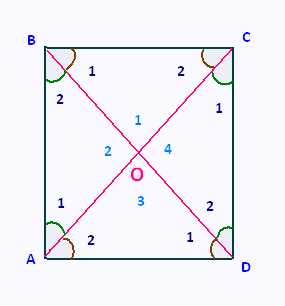
ABCD est un carré.
Démontrer que ses diagonales sont perpendiculaires.
Solutions
|
|