Mathématiques 2: Exercices & problèmes divers
1. Exercices sur le rectangle
1.1. Aire maximale dans un rectangle
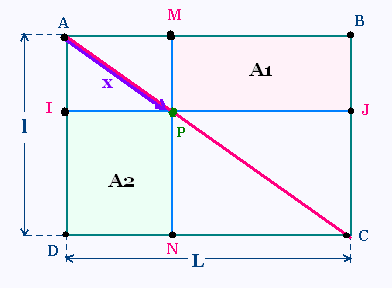
On considère un rectangle de longueur L
et de largeur l. Sur une diagonale on
déplace un point P d'une distance x
à partir du smmet A. On obtient
deux rectangles d'aires A1 et A2.
a) Montrer que les deux aires A1 et A2 sont
égales.
b) Ou faut-il placer le point P pour que l'aire
commune (A1 = A2) soit maximale?
1.2. Rectangle: resolution de problèmes
La base d'un rectangle mesure 7 cm de plus que
la mesure de la hauteur. Le périmètre de ce
rectangle est 30 cm. Quelles sont les mesures
de la hauteur et de la base de ce rectangle?
2. Expressions algébriques
2.1. Répondre aux questions suivantes
Soit l'expression algébrique suivante:
4x2 - 10 y2 - 8 xy + 4 y2 + 12.
a) Quel est le terme constant de cette expression?
b) Quel est le coefficient du 3e terme?
c) Quel est le degré de ce polynôme?
2.2.Réduire les expressions suivantes
a) 2 a - 4 + 6a =
b) 3 x - 5,5 - 1.5 x + 2 =
c) 8 x + 2 - 7 x + 2 y =
d) 2 a - 5 b + 12 b - 3 a =
e) 2 xy + x - xy + 5 y =
f) 5 bc - 2 b - (3 bc - 9 b) =
g) 1.2 x + 2.8 y - xy - 1.8 y + 0.8 x =
h) 3x/2 + 4/5 - 5x/4 - 1/2 =
i) 6 xy - 5 x2y + 7 yx - (- 12 x2y + 3 xy) =
2.3. Suites numériques linéaires
a) Compléter la suite suivante :
| rang n | 1 | 2 | 3 | 4 | 5 |
| terme t | 5 | 8 | 11 | ... | ... |
b) Déterminez la règle qui permet de calculer
la valeur d'un terme y selon son rang n.
2.4. Suites numériques quadratiques
a) Compléter la suite suivante :
| rang n | 1 | 2 | 3 | 4 | 5 |
| terme t | 6 | 9 | 14 | .. | ... |
b) Déterminez la règle qui permet de calculer
la valeur d'un terme y selon son rang n.
2.5. Représentation graphique d'une
suite linéaire
à partir des tables de valeurs
Représentater graphiquement les deux suites linéaires
suivantes:
a)
| x | 1 | 2 | 3 | 5 | 10 |
| y | 5 | 7 | 9 | 13 | 23 |
Est- elle croissante ou decroissante?
b)
| x | 0 | 1 | 2 | 3 | 5 |
| y | 5 | 2 | - 1 | - 4 | - 10 |
Est- elle croissante ou decroissante?
3. Exercices sur le théorème de Pythagore
3.1. Vérifier si un triangle est rectangle
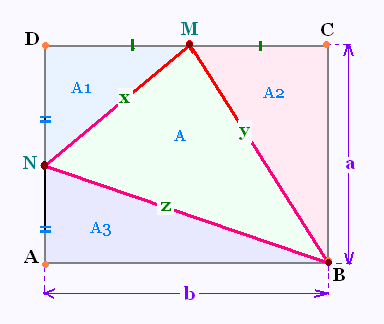
Soit un rectangle ABCD de largeur a et de
longueur b.
Le point M est le milieu de côté CD,
le point N est le milieu du côté AD.
a) calculer l'aire du rectangle ABCD.
b) Calculer les aires A1, A2 et A3 des trois
triangles NDM, MCB et ABN respectivement.
c) En déduire l'aire du triangle MNB
d) On pose:
BN = h
NM = x
MB = y
Calculer le carré du côté h, x et y
e) Utiliser le théorème de Pythagore pour
montrer que le triangle NBM n'est pas rectangle.
f) Donner le pourcentage des aires A1, A3 et A
par rapport à l'aire du rectangle ABCD.
g) Quelle doit être la relation entre les côtés
a et b pour que le triangle NMB soit rectangle.
3.2. Trouver une hypoténuse
Trouver x dans la situation suivante:
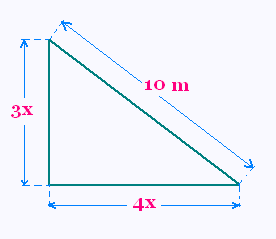
4. Tracés des trapèzes
Tracer quatre trapèzes identiques
à l'intérieur d':
a) un rectangle,
b) un trapèze.
Solutions
|



