Mathématiques 2: Algèbre:
Problèmes du 1er degré
Inégalités et inéquations
Concours de lecture

Compétition de lecture

William et Helena participent à un cncours de lecture d'un roman de 800 pages.

La vitesse de lecture "A" de William est comprise entre 150 et 190 livres par jour. Celle d'Helena "B" est comprise entre 160 et 200 livres par jour.

Au commencement de la compétition, William avait déjà lu 500 pages et Helena avait déjà lu 400 pages.

Montrer qu'Helena ne pourra jamais finir la lecture du roman avant William.

soit x le nombre de jours que les deux candidats doivent mettre pour finir la lecture du roman.

On a donc:

800 = 500 + A x
800 = 400 + B x

ou

300 = A x
400 = B x

On a aussi

150 < A < 190 et
160 < B < 200

C'est à dire

150 < 300/x < 190 et
160 < 400/x < 200

On défait chaqcun des deux encadrements pour obtenir les inégalités suivantes:

• 150 < 300/x
• 300/x < 190 et
• 160 < 400/x
• 400/x < 200

• Première inéquation:

On multiplie ses deux membres par x qui est positif et on divise par 150 qui est positif. Le sens de l'inéquation ne change pas. On obtient:

150 x < 300
x < 300/150

On fait un calcul similaire pour les trois autres, puis on refait l'encadrement et on obtient:

300/190 < x < 300/150
400/200 < x < 400/160

C'est à dire

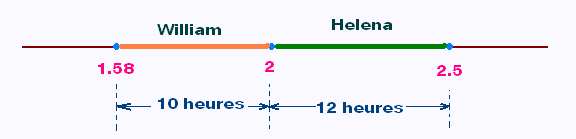
1.58 < x < 2
2 < x < 2.5

William mettra entre (1 jour + 14 heures) et (2 jours) pour finir le roman. Helena mettra entre (2 jours) et (2 jours et demi).

Willian finira le roman bien avant Helena.

En termes d'heures, on aura 10 heures pour Willian et 12 heures pour Helena: