Mathématiques
2
Problèmes du
1er degré
© The scientific sentence. 2010
|
Mathématiques 2: Algèbre:
Problèmes du 1er degré
Inégalités et inéquations
Course de vélo
Course en vélo
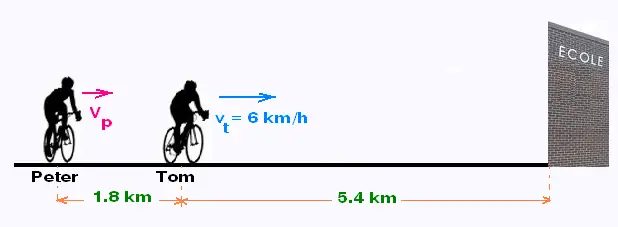
En vélo, Tom roule à une vitesse de 6 km/heure. Il
ne lui reste que 5.4 km pour arriver à l'école.
En ce momemt, Peter est à 1.80 km derrière Tom.
À quelle vitesse vp Peter doit rouler pour
rattraper Tom avant l'école ?
Il reste à Tom t = (5.4 km)/(6 km/h) = 0.9 heures pour arriver
à l'école.
Pour rattraper Tom, Peter doit faire au plus ce temps de
0.9 heures, soit un temps inférieur à 0.9 heures.
Ainsi Peter doit parcourir au plus la distance:
vp x t = 1.80 + 5.4 = 7.2 km. Soit
t = 7.2/vp.
On a donc
t < 0.9
D'où
7.2/vp < 0.9 , ou
vp > 7.2/0.9 = 8 km/h.
Pour rattraper Tom avant l'école, la vitesse
requise pour Peter, doit être supérieure à 8 km/h.
Interprétation
Pour le temps t = 0.9 heures:
- Tom roulera 5.4 km . Il arrivera à l'école.
- Pour Peter trois cas sont possibles:
• Si sa vitesse vp = 7.5 km/h (< 8 km/h),
il roulera 7.5 x 0.9 = 6.75 km < 7.2 km.
Il ne rattrapera donc pas Tom.
• Si sa vitesse vp = 8 km/h, il roulera
8 x 0.9 = 7.2 km.
Il arrivera donc en même temps à l'école que Tom.
• Si sa vitesse vp = 8.5 km/h (> 8 km/h),
il roulera 8.5 x 0.9 = 7.65 km > 7.2 km.
Il rattrapera Tom avant l'école.
À cette vitesse de 8.5 km/h de Peter, lorsque Tom aura
parcouru une distance x en un temps t = x/6, Peter aura
parcouru 1.8 + x pour un même temps t = (1.8 + x)/8.5.
On a donc:
t = x/6 = (1.8 + x)/8.5 , d'où
8.5 x = 6(1.8 + x) = 10.8 + 6 x
8.5 x - 6 x = 10.8
x = 10.8/2.5 = 4.32 km
Tom aura parcouru x = 4.32 km ,
Peter aura parcouru 1.8 + 4.32 = 6.12 km.
Ainsi, à cette vitesse de Peter de 8.5 km/h, Tom
sera rattrapé par Peter lorsqu'il restera
5.4 - 4.32 = 1.8 km de l'école.
Avec une vitesse vp = 10 km/h, On aura :
t = x/6 = (1.8 + x)/10 , d'où
10 x = 6(1.8 + x) = 10.8 + 6 x
10 x - 6 x = 10.8
x = 10.8/4 = 2.70 km
Ainsi, à cette vitesse de Peter de 10 km/h, Tom
sera rattrapé par lorsqu'il restera
5.4 - 2.7 = 2.7 km de l'école.
|
|