Mathématiques 2: Équations du premier degré s

Deux photocopieurs

1. Fonctions directes

Deux photocopieurs sont utlisés.

Un photocopieur A mets 5 secondes pour démarrer est produit une copie en 3 secondes, et

Un photocopieur B mets 8 secondes pour démarrer est produit une copie en 7.2 secondes.

Combien produisent ses deux machines et en combien de temps?


Solution


Les deux photocopieurs A et B sont mis en marche tous les deux en même temps au même instant initial t = 0.

Pour le photocopieur A:

Après 5 secondes le photocopieur A commence à produire les photocopies. Il produit 0 copies pendant les 5 premières secondes et "x" copies pendant un certain temps tA, à raison de trois secondes par copie, de telle sorte que le temps t total sera égal à:

t = 5 + tA ou

f(x) est le temps en secondes et 3 est le temps en secondes par copie. x est le nombre de copies.

On compte le temps par nombre de copies. t est la variable dépendente et x est la variable indépendente.

Pour le photocopieur B:

Après 8 secondes le photocopieur B commence à produire les photocopies. Il produit 0 copies pendant les 8 premières secondes et "y" copies pendant un certain temps tB, à raison d'une copie par 7.2 secondes, de telle sorte que le temps t total sera égal à:

t = 8 + tB ou

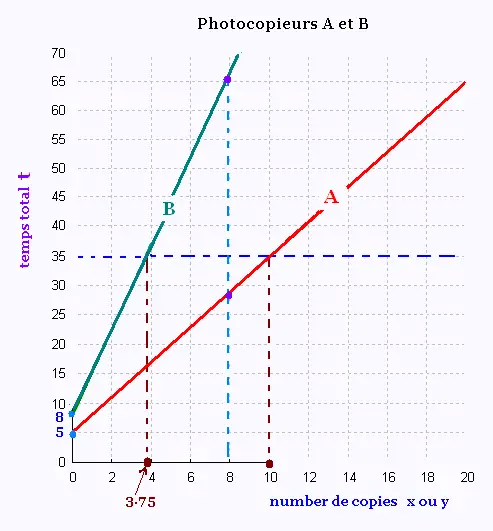
Dans le graphe suivant, on représente le temps total t en fonction du nombre de copies produites par A ou par B.





Les photocopieurs A et B ne produiront jamais un même nombre de copies pour un même temp de fonctionnement. Le photocopieur A est toujours plus rapide que le B.

Par exemple:

a) Pour un temps de 35 secondes, le photocopieur A produit 10 copies tandis que le photocopieur B ne produit que 3,75 copies.

b) Pour 8 copies, le photocopieur A mets 29 secondes pour les produire, tandis que le photocopieur B mets 65.6 secondes pour produire ces 8 copies.

2. Fonctions réciproques

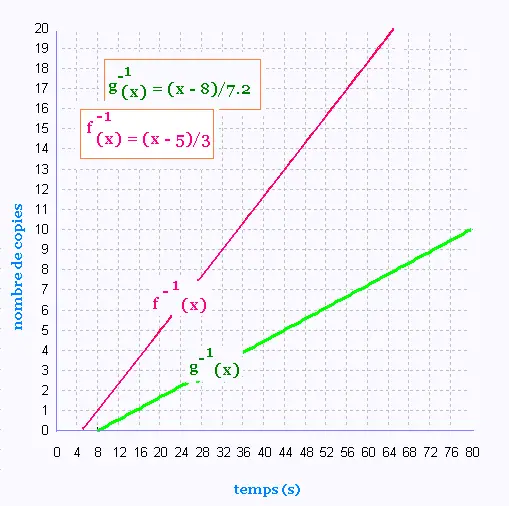
Les réciproques des fonctions f et g sont:

f^-1(x) = (x - 5)/3
g^-1 (x) = (x - 8)/7.2

Ces fontions donnent le nombre de copies en fonction du temps.