Mathématiques
2
Problèmes du
1er degré
© The scientific sentence. 2010
| Mathématiques 2: Algèbre:
Problèmes du 1er degré
Satellite sur orbites
Satellite sur orbites
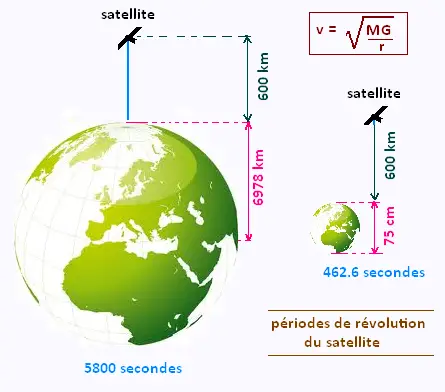
La vitesse d’injection d'un satellite sur une orbite circulaire
est donnée par la formule:
v = √(M.G/r)
La vitesse et le rayon d'orbite du satellite ne sont pas proportionnels.
Le carré de la
vitesse est inversement proptionnel au rayon d'orbite.
G = constante de gravitation
= 6,674 x 10-11 N.m2.kg-2 =
6.674 x 10-11m3.kg-1.s-2
M = masse de la Terre = 5,972 x 1024 kg
r = rayon d'orbite = distance: satellite–centre de la Terre
= altitude + rayon de la terre.
Rayon de la terre = 6 378 000 m .
La formule si-dessus donne:
1. Pour une atitude de 600 km et un
rayon de la terre = 6 378 000 m
, on a :
r = 6 378 + 600 =
6978 km = 6978 000 m .
La vitesse du satellite est v = 7558 m/s =
2.721 x 104 km/h
La circonférence de l'orbite du satellite est :
C = 2 π r = 2 x π x 6978 000 m = 4.384 x 107 m
Ce qui correspond à 4.384 x 107/7558 s =
5800 secondes.
La période de révolution du satellite est de
5800 secondes.
2. Pour une atitude de 600 km et
un diamètre de la terre = 75 cm , on
aurait;
Le rayon de la terre serait de 37.5 cm = 0.000375 km =
3.75 x 10- 4 km.
Pour une même atitude de 600 km, on aurait r = 600 + 0.000375 =
6 00 km =
600 000 m.
La vitesse du satellite serait v = √(39.857 x 1013/600 000) =
√(6.643 x 107) = 8.15 x 103 m/s =
8150 m/s.
La circonférence de l'orbite du satellite serait:
C = 2 π r = 2 x π x 600 000 m = 3.77 x 106 m
Ce qui correspondrait à 3.77 x 106/8150 s = 462.6 secondes.
La période de révolution du satellite serait de
462.6 secondes.
|
|