Mathématiques 2: Équations du premier degré

Deux voitures roulant en sens inverse

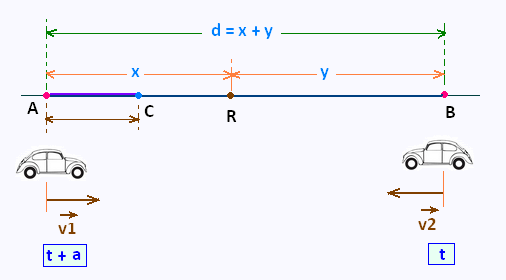
Deux voitures A et B se rencontrent au point R.
La voiture A démarre à 10 h 20 du point A, et roule à une vitesse constante v1 = 227 km/h.

La voiture B démarre du point B, 10 mn plus tard, et roule à une vitesse constante v2 = 239 km/h.

La distance qui les sépare, au départ, c'est à dire la distance AB mesure d = x + y = 220 km.

Question

Quand et où ces deux voitures vont-elles se rencontrer?

Réponse:

On prend l'origine du temps celui de la voiture A.

L'équation du mouvement de la voiture A est: x = v1 t

Celle de la voiture B est: y = v2(t - 10 mn)

On sait que x + y = z, donc y = z - x. Donc

z = x + y = v1 t + v2(t - 10 mn) = (v1 + v2)t - 10 v2

t = (z + 10v2)/(v1 + v2)

t = [220 + (10/60) x 239]/(227 + 239) = 0.56 h = 33 mn 27 s.

Pour A, la rencontre aura lieu dans 33 mn 27 s après son démarrage. Pour B, c'est 10 mn plus tard, soit 23 mn 27 s.

x = v1 t = 227 x 0.56 = 127.12 km.

y = z - x = 220 - 127.12 = 92.88 km.

Pour A, la rencontre aura lieu à la distance 127.12 km du point A. Pour B, c'est à 92.88 km du point B.

Remarque

Si on prend l'origine du temps celui de la voiture B, on aura:

L'équation du mouvement de la voiture B est: y = v2 t

Celle de la voiture A est: x = v1(t + 10 mn)

z = x + y = v2 t + v1(t + 10 mn) = (v1 + v2)t + 10 v1

t = (z - 10v1)/(v1 + v2)

t = [220 - (10/60) x 227]/(227 + 239) = 0.39 h = 23 mn 27 s.

Pour B, la rencontre aura lieu dans 23 mn 27 s après son démarrage. Pour A, c'est 10 mn plus tôt, soit 33 mn 27 s.