Mathématiques 2: Algèbre
Fonction partie entière
Graphique et règle

On peut tracer le graphique d’une fonction partie entière en utilisant:

• un texte qui decrit une mise en situation,
• une table de valeurs, ou
• une règle.

On peut également déterminer la règle d’une fonction partie entière en utilisant:

• un texte qui decrit une mise en situation,
• une table de valeurs,
• un graphique.

1. Tracer le graphique à partir
d’une mise en situation

Exemple 1

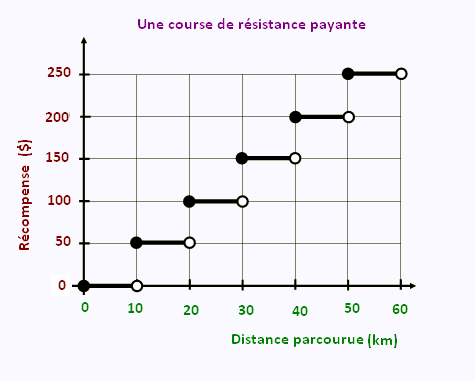
Dans une course à pieds de résistance non-stop, le coureur est payé 50 $ pour chaque tranche de 10 km effectuée.

Pour tracer le graphique représentant cette situation, il faut analyser le texte.

Variable indépendante (x) : la distance parcourue(km). Variable dépendante (y) : la récompense ($).

La valeur initiale est 0, car s’il n’y a aucun déplacement, il n’y a aucune récompense.

Chaque marche aura une longueur de 10 unités, fermée à gauche, car il faut avoir complété chaque tranche de 10 km pour obtenir la récompense.

La distance verticale entre chaque marche sera de 50 unités; comme il y aura accumulation, la fonction sera croissante ( a > 0 ).

h = 0, k = 0
a = longueur de la contremarche = 50
longueur de la marche = 10 b > 0

Utiliser du papier quadrillé pour tracer une fonction partie entière, c'est plus pratique.

Exemple 2

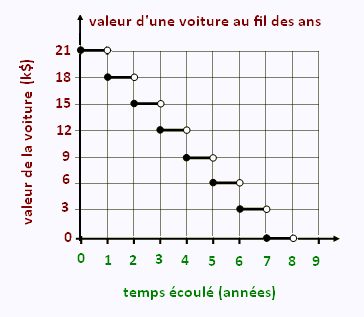
La voiture de Johnny coûte 21 000 $. Elle perd chaque année 3000 $ = 3 k$ de sa valeur.

On analyse le texte.

Variable indépendante (x) : le nombre d'années.
Variable dépendante (y) : la valeur de la voiture ($).

La valeur initiale est 21 k$, car au début,
la valeur de la voiture était de 21 k$.

Chaque marche aura une longueur de 1 unité, fermée à gauche, car il faut que l'année soit complété pour que la valeur de la voiture diminue.

La distance verticale entre chaque marche (contremarche) est de 3 unités; comme il y aura dévalorisation la fonction sera décroissante ( a < 0 ).

h = 0, k = 21
a = - 3
longueur de la contremarche = 3
longueur de la marche = 1
b > 0

2. Tracer le graphique à partir d’une table de valeurs

Il est très facile de tracer le graphique d’une fonction partie entière quand on connaît la table de valeurs associée à la situation.

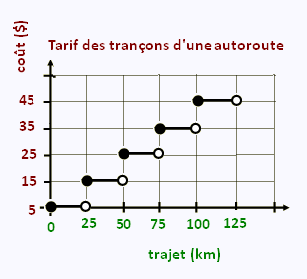
Le tableau suivant indique le coût des trajets dans une autoroute selon le tronçon effectué.

tronçon (km)	coût ($)
variable indépendente	variable dépendente
[0,25[	5
[25,50[	15
[50,75[	25
[75,100[	35
[100,125[	45

La fonction est croissante, donc a > 0; l’augmentation est de 10 unités, donc | a | = 10.

Les crochets indiquent que les bornes des segments sont pleines à gauche et vides à droite, donc b > 0.

La largeur des marches est de 25 unités, donc | b | = 1/25.

La première classe débute à 0, donc h = 0.

La valeur initiale est 5 et h = 0, donc k = 5.

a = 10, b = 1/25, h = 0, et k = 5

3. Tracer le graphique à partir de la règle

Pour tracer le graphique d’une fonction partie entière à partir de la règle de la fonction, on doit bien comprendre chaque paramètre.

Sous forme canonique, la fonction partie entiere s'ecrit:

f(x) = a [b(x – h)] + k

1. Le paramètre a :

• donne la distance verticale entre les marches, c'est à dire la contremarche,
• se calcule en valeur absolue : |a|, puisqu'une distance est toujours positive;

si a > 0, la fonction est croissante;
si a lt; 0, la fonction est décroissante.


2. Le paramètre b : :

• indique si l’intervalle (marche) est ouvert à gauche ou à droite;
b > 0
b < 0

• il donne la longueur des marches (intervalles);
• il se calcule en valeur absolue : |b|, car une longueur est toujours positive.

Du fait que la marche de la fonction partie entière de base mesure est 1 unité, donc
• Si b > 1, on atteint la partie entière plus rapidement; ce qui diminue la longueur de la marche.
• Si 0 < b < 1, on atteint la partie entière moins rapidement, ce qui augmente la longueur de la marche.

La longueur d'une marche est égale à 1/|b|.

3. Les paramètres h et k :

Ces deux paramètres correspondent à la borne pleine des marches.

Exemple:

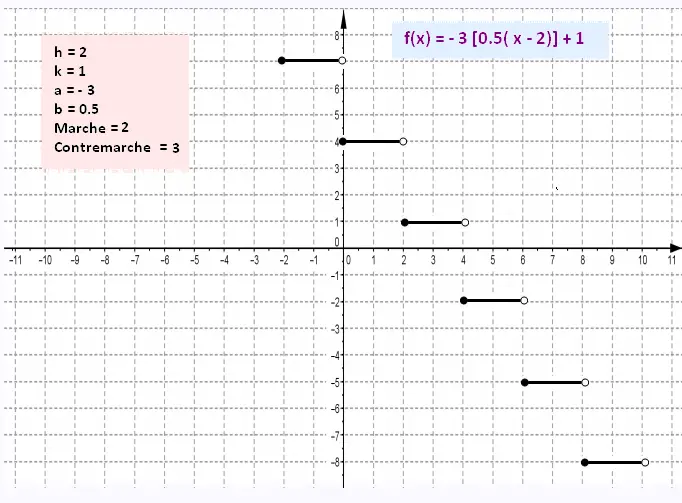
Soit tracer le graphique de la fonction

f(x) = - 3 [0.5( x - 2)] + 1

Étape 1 : Déterminer la valeur des paramètres :

h = 2 , k = 1, a = - 3, b = 0.5.

contremarche = 3, marche = 1/0.5 = 2.

Étape 2 : Interpréter les paramètres:

a et b sont de signes contraires, donc la fonction est décroissante;

a = - 3, |a| = 3, donc la distance entre les marches est de 3 unités;

b = 0.5, donc la longueur des marches est de 1/|b| 1/0.5 = 2
b > 0, donc les segments sont fermés à gauche;

h = 2, donc il n’y a une translation horizontale de 2 unités vers la droite;
k = 1, donc il y a translation verticale de 1 unités vers le haut.

Étape 3 : Tracer le graphique:

1) On commence par placer une borne pleine en utilisant (h , k) = (2, 1),

2) On détermine la longueur et l’orientation d’un segment à l’aide de la valeur de b.
marche = 1/|b| = 2. b > 0 donc :


3) On répète les segments en utilisant la valeur de a
a < 0 et | a | = | - 3| = 3. On monte vers le haut de trois unités.

Les extrémités des marches doivent toujours être vis-à-vis les unes des autres.

4. Déterminer la règle en utilisant un
texte (une mise en situation)

Exemple 1:

Mise em situation: Dans une course à pieds non-stop, le coureur est payé 50 $ pour chaque tranche de 10 km effectuée.

Il faut analyser le texte.
Variable indépendante (x) : la distance parcourue (km).
Variable dépendante (y) : la récompense ($).

La valeur initiale est 0, car s’il n’y a aucune distance parcourue, il n’y a aucune récompense: h = 0, k = 0

Chaque marche (intervalle) aura une longueur de 10 unités, fermée à gauche, car il faut avoir complété chaque tranche de 10 km pour obtenir la récompense. Donc, b = 1/10 = 0.1

La distance verticale entre les marches sera de 50 unités; comme il y aura accumulation, la fonction sera croissante (a> 0).

a = 50
b = 0.1
h = 0
k = 0

f(x) = 50[0.1(x - 0] + 0

f(x) = 50 [x/10]


Exemple 2:

La voiture de Johnny coûte 21 000 $. Elle perd chaque année 3000 $ = 3 k$ de sa valeur.

Il faut analyser le texte.

Variable indépendante (x) : le nombre d'années.
Variable dépendante (y) : la valeur de la voiture ($).

La valeur initiale est 21 , car au début, la valeur de la voiture était de 21 k$.

h = 0 et k = 21

Chaque marche (intervalle) aura une longueur de 1 unité, fermée à gauche, car il faut que l'année soit complété pour que la valeur de la voiture diminue.

donc b = 1/longueur d’une marche = 1/1 = 1

La distance verticale entre les marches sera de 3 unités; comme il y aura diminution, la fonction sera décroissante (a < 0).

a = 3 < 0
b = 1 > 0
h = 0
k = 21

f(x) = - 3 [1 ( x - 0)] + 21

f(x) = - 3 [x] + 21

5. Déterminer la règle en utilisant une
table de valeurs

Le tableau suivant indique le coût des trajets dans une autoroute selon le tronçon effectué.

tronçon (km)	coût ($)
variable indépendente	variable dépendente
[0,25[	5
[25,50[	15
[50,75[	25
[75,100[	35
[100,125[	45

Les crochets indiquent que les bornes des segments sont pleines à gauche et vides à droite donc: b > 0.

La largeur des classes est de 25 unités donc |b| = 1/ largeur d’un intervalle = 1/25 = 0.04

La première classe débute à 0 et la valeur initiale est 5, donc h = 0 et k = 5

La distance verticale entre les marches sera de 10 unités, car le coût sur l'autoroute augmente de façon régulière à chaque changement d’intervalle: a = 10 > 0.
a = 10
b = 0.04
h = 0
k = 5

f(x) = 10[0.04(x - 0)] + 5

f(x) = 10[x/25] + 5

6. Déterminer la règle en utilisant un graphique

Déterminer la règle à partir d’un graphique est le moyen le plus facile.

Il s’agit simplement de bien comprendre les paramètres de la fonction.

Exemple 1



En utilisant la borne pleine de la marche la plus près de l’origine, on constate que h = 0 et k = 0

b > 0, car le segment est fermé à gauche.
b = 1/longueur d’une marche = 1/10 = 0.1.

a > 0, car la fonction est croissante et b > 0. |a| = 50.

f(x) = a [ b (x – h) ] + k

f(x) = 50[0.1(x - 0)] + 0

f(x) = 50[x/10]

La fonction partie entière possède plusieurs marches.

Pour déterminer la valeur de h et de k, il y a donc plusieurs possibilités.

Par exemple: h et k pourraient être h = 10, et k = 50 ou (30, 150) ou (50, 250).

Il y a plusieurs possibilités, donc plusieurs règles possibles

• f(x) = 50[x/10]

• f(x) = 50[0.1(x - 30)] + 150

• f(x) = 50[0.1(x - 50)] + 250

Pour déterminer les différentes valeurs de f(x) pour des valeurs de x, toutes ces règles sont équivalentes.

• f(x) = 50[x/10]
f(20) = 50[20/10] = 100

• f(x) = 50[0.1(x - 30)] + 150
f(20) = 50[0.1(20 - 30)] + 150 = - 50 + 150 = 100

• f(x) = 50[0.1(x - 50)] + 250
f(20) = 50[0.1(20 - 50)] + 250 = - 150 + 250 = 100

Pour éviter la lourdeur des calculs, on détermine h et k avec une marche près de l’origine; on travaille ainsi avec des paramètres plus petits.


Exemple 2

Détermine les règles des graphiques suivants :




h = 0, k = 21.
b > 0, car
|b| = 1/ longueur d’une marche = 1/1 = 1. Donc b = 1.

a < 0, car la fonction est décroissante et b > 0.
|a| = 3 donc a = - 3.

f(x) = a [ b (x – h) ] + k

f(x) = - 3 [ 1 (x – 0) ] + 21

f(x) = - 3 [x ] + 21



Autres exemples
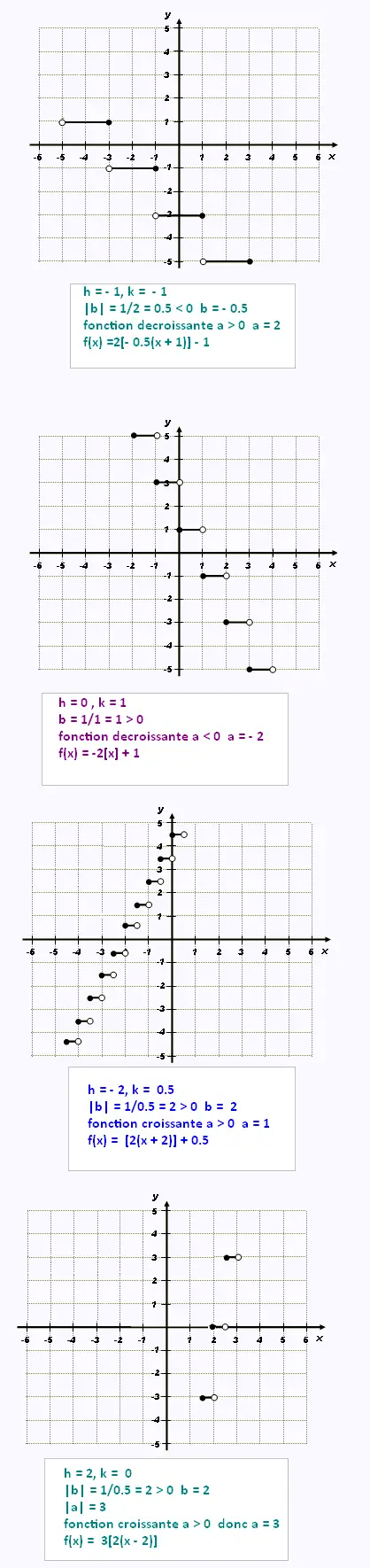