Maths
- 2 -
Fonction en escalier
Fonction partie entière
Exercices
© The scientific sentence. 2010
| |
Mathématiques 2: Fonctions
Fonction partie entière
Résolutions d'équations
1. Propriété à utiliser
[x] ≤ x < [x] + 1
Cette propriété est utile pour retrouver les valeurs de x quand
on connaît une valeur de f(x), c’est à dire résoudre l'équation
[x] = n où n est un nombre donné.
2. Exemples de résolution des équations
avec la partie entière
Exemple 1:
Résoudre l'équation: 1 + [0.20 x] = 4
En premier, il faut isoler la partie entière:
[0.20 x] = 4 - 1 = 3
[0.20 x] = 3.
On applique la propriété pour l'expression entre les crochets:
3 ≤ 0.20 x < 4
30/2 ≤ x < 40/2
15 ≤ x < 20
L'ensemble de solutions est:
S = [15, 20[
Exemple 2:
425 = - 25 [ x ] + 500
25 [ x ] = 500 - 425
25 [ x ] = 75
[ x ] = 3
3 ≤ x < 4
L'ensemble de solutions est:
S = [3, 4[
Remarque:
L'ensemble des solutions d'une fonction en escalier
est un intervalle.
2. Résolution des équations
avec la partie
entière cas général:
f(x) = a [ b (x – h) ] + k
0 = a [ b (x – h) ] + k
- k = a [ b (x – h) ]
- k/a = [ b (x – h) ]
• Si - k/a ∉ Z, il n’y a aucun zéro.
• Si - k/a ∈ Z, , il y a une infinité de zéros.
Il peut donc arriver qu’une fonction partie entière
n’ait pas de zéro.
Exemple :
f(x) = -2 [ x ] + 1 n'a aucun zéro.
f(x) = -2 [ 0,5 (x – 1) ] - 2 a une infinité de zéros.
3. Autres exemples sur la résolution des
équations
avec la partie entière
Un graphique permet de déterminer des valeurs de f(x) lorsqu’on
connaît une valeur de x
• Dans le graphique ci-dessous par exemple, que vaut f(x) quand x vaut 25 ?
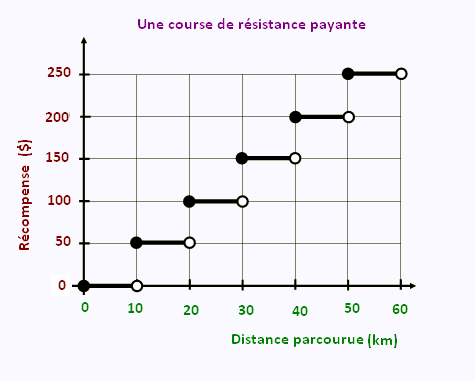
À la lecture du graphique, on peut constater que lorsque x = 25,
f(x) = 100.
On peut calculer cette valeur en utilisant la règle de la fonction:
f(x) = 50 [ 0.1 x ]
f(25) = 50 [(0.1) (25)] = 50 [2.5] = 50 x 2 = 100
Le graphique permet aussi de trouver les valeurs
de x lorsqu’on connaît une valeur de f(x).
• Dans le graphique ci-dessous, que vaut x quand f(x) vaut 200?
On peut constater que lorsque f(x) = 200, x est compris entre [ 40, 50[.
On peut calculer cette valeur en utilisant la règle:
f(x) = 50 [ 0.1 x ] = 200
[ 0.1 x ] = 200/50 = 4
L’expression « partie entière » (entre les crochets) d
oit être supérieure ou égale à l’entier inférieur (ici 4),
et inférieure à l’entier supérieur (ici 5).
On doit donc résoudre les deux inéquatons:
0.1 x ≥ 4 , donc x ≥ 40
0.1 x < 5, donc x < 50
40 ≤ x < 50
Sur une droite numérique , on trouve très rapidement
x ∈ [40, 50[.
Pour déterminer les valeurs associées à une équation partie entière,
on peut toujours utiliser le graphique, mais ce dernier n’est
pas toujours le meilleur moyen.
Procéder algébriquement en utilisant la règle de la fonction est souvent plus efficace.
La règle permet de calculer d’autres valeurs qui ne sont pas
représentées sur le graphique.
Que vaut f(x) quand x vaut 70 par exemple?
f(x) = 50 [ 0.1 x ] = 50 [ (0.1)(70) ] = 50 x 7 = 350.
4. Type de Problèmes relatifs à la partie entière
On rencontre des problèmes variés relatifs à la fonction en escalier et
particulièrement à la partie entière. Voici un exemple.
Jim décide d'économiser de l'argent. Il se fixe
la règle suivante : Pour chaque dollar x gagné, il
doit économiser y = 3 + [x/12]
a) Si Jim gagne 240 $, combien doit-il économiser ?
b) Si 53 $ doivent être économiés, combien
Jim devrait-il gagner?
a) y = 3 + [x/12] = 3 + [240/12] = 3 + 20 = 23 $.
Réponse : Jim aurait économisé 23 $.
b) 53 = 3 + [x/12]
[x/12] = 50
50 ≤ x/12 < 51
50 x 12 ≤ x < 51 x 12
600 ≤ x < 612
Réponse : Jim devrait gagner entre 600 et 612 $.
|
|