Mathématiques 2: Fonctions
Fonction en escalier
Introduction et exemples

1. Definitions

    On trouve des fonctions en escalier dans la vie courante. Les impôts, les frais de garderie, le stationnement des véhicules, les primes en fonction des ventes dans une entreprise, les frais de scolarité dans les écoles, les primes d'assurance, etc ...

Les fonctions en escalier servent à représenter des situations dans lesquelles la variable dépendante reste constante pendant une certaine variation de la variable indépendante.

On les appelle ainsi à cause de leur forme ressemblant à un escalier. La partie horizontale est appelée marche, et la partie verticale contre marche.

Une fonction en escalier est une fonction qui est constante sur des intervalles de la variable indépendante et qui change brusquement pour certaines valeurs de cette variable indépendante, appelées valeurs critiques.

Le graphique de la fonction en escalier sur un plan cartésien est formé de segments ou paliers horizontaux, habituellement fermés à une extrémité (borne pleine) et ouverts à l'autre (borne vide).

La courbe d'une fonction en escalier ne peut être tracée sans lever le crayon, on dit que la fonction est discontinue.

Il faut toujours lire attentivement la mise en situation pour bien représenter les informations.

2. Exemples

Exemple 1: L'impôt fédéral canadien

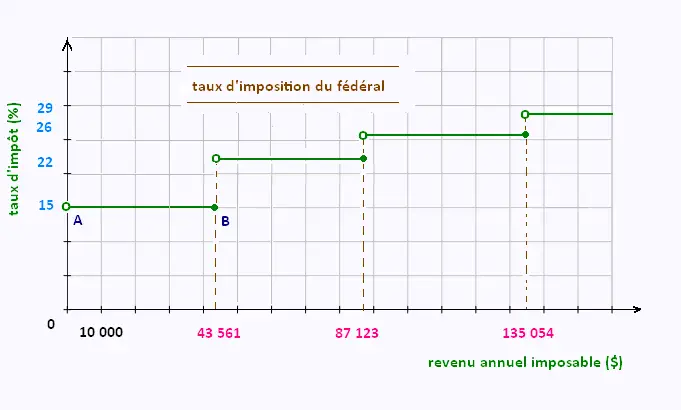
Le taux d’imposition payé au gouvernement est une fonction en escalier.

Sur un même intervalle, la variable indépendante varie mais la variable dépendante est constante.

Entre 43 561, et 87 123 $; le pourcentage d'impôt est constant, soit 22%.

La borne de la première marche [AB] est vide, car si on n'a pas de revenu, on ne paie pas d’impôt.

La borne B est pleine, car à 43 561 $, on paie encore 15% du revenu.

Les valeurs de la variable indépendante pour lesquelles la fonction varie subitement sont dites valeurs critiques. Ici, les valeurs critiques sont { 43 561, 87 123, 135 054 }.

Exemple 2: Location d'un camion Uhaul

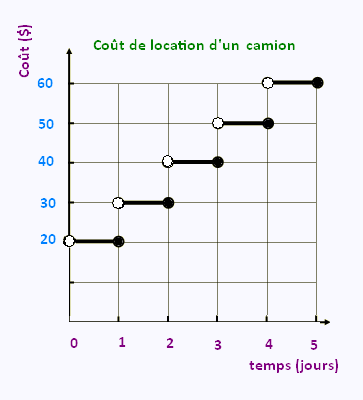Le coût de location d'un camion (de type Uhaul, Budget) varie selon la durée de location.

La premier jour coûte 20 $ et les jours supplémentaires coûtent 10.0 $ le jour.

Qu’on utilise le camion pendant 1 heure, ou 2 heures, ou 5 heures, ou 15 heures, ou 24 heures, le coût est toujours 20 $.

De 24 heures (1 jour) et une seconde jusqu’à deux jours, le coût passe subitement à 30.0 $.

Voici le tableau de valeur de cette situation:

Coût de location d’un camion
x	y
Durée de location (j)	Frais de location ($)
] 0, 1 ]	20
] 1, 2 ]	30
] 2, 3 ]	40
] 3, 4 ]	50
] 4, 5 ]	60

Le graphique de cette situation est représenté ci-haut. Il représente également cette table de valeurs.

La variable indépendante (x) représente la durée de location. La variable dépendante (y) représente le coût de location.

Le premier intervalle de la variable indépendante ] 0, 1 ] correspond à 1 jour.

La location du camion coûte 20 $ pour 1 heure, 2 heures, 10 heures, 20 heures, ou 24 heures.

Dans cet intervalle d'une journée, la variable indépendante (x) varie, mais la variable dépendante (y) ne varie pas.

Dans l’intervalle ] 0, 1 ], ce crochet est ouvert pour exclure 0, puisqu’à 0 seconde, il n’y a pas de frais de location; à partir de la première seconde, le tarif sera de 20.00 $.

Ce crochet est fermé pour inclure 1, car jusqu’à concurrence d'un jour, le tarif sera le même.

Dans l’intervalle ] 1, 2 ], ce crochet est ouvert pour exclure le 1, puisque le 1 fait déjà partie de l’autre intervalle.

À partir de 1 heure et 1 seconde, le tarif sera de 30,00 $.

Ce crochet est fermé pour inclure 2, car jusqu’à concurrence de 2 heures, le tarif sera le même.

Et ainsi de suite...

Sur le premier segment, la borne est vide, car le crochet est ouvert; 0 est exclus.

À l’autre extrémité du segment, la borne est pleine, car le crochet est fermé; 1 est inclus.

Selon les situations à représenter, les bornes peuvent être disposées autrement: o-• ou •-o.

Exemple 3: Frais de scolarité à l'école Les escaliers

Voici le tableau des frais de formation à l'école «Les escaliers». Cette formation dure 5 ans.

Frais de scolarité
x	y
Niveau de formation (a)	Frais de formation (k$)
] 0, 1 ]	4
] 1, 2 ]	4.5
] 2, 3 ]	5
] 3, 4 ]	5.5
] 4, 5 ]	6

Les frais de scolarité en fonction du nombre d'années de formation, dans cette école, est une fonction en escalier.



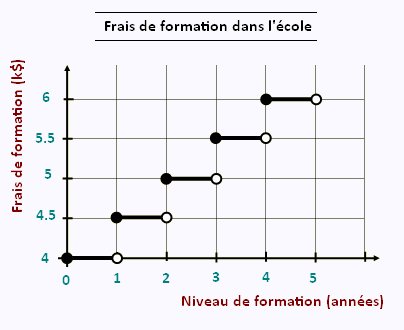
Au point (0, 4), la borne est pleine, car dès l’engagement, l'étudiant paye 4 000 $.

Au point (1, 4) la borne est vide, car c'est dès le début de la deuxième année que l'étudiant payera 4 500 $.

3. Forme canonique d'une fonction en escalier

La forme canonique d'une fonction en escalier est la suivante:


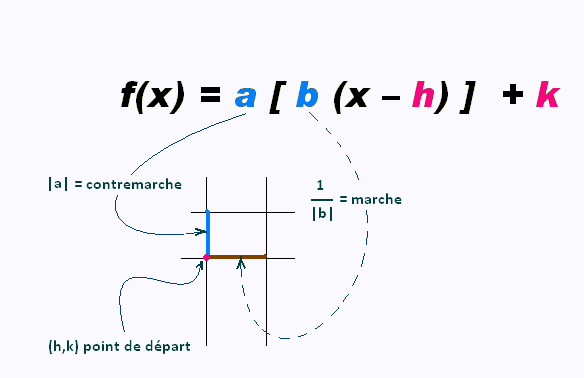
Les paramètres du point de départ h et k sont toujours fixés.

Dans une fonction en esclaier les paramètre a et b peuvent varier.

Mais pour une fonction partie-entière, ces deux paramètres a et b sont fixés.