Maths
- 2 -
Fonction en escalier
Fonction partie entière
Exercices
© The scientific sentence. 2010
| |
Mathématiques:
Fonction en escalier
Fonction partie entière
Exercice 1
Trouver la marche, la contremarche, le sens
du segment et la varuation des fonctions suivantes:
f1(x) = 2[x/4], f2(x) = -[0.5 x] , f3(x) = - 3[-x] ,
et f4(x) = [- x/2] .
1) Marche et contremarche:
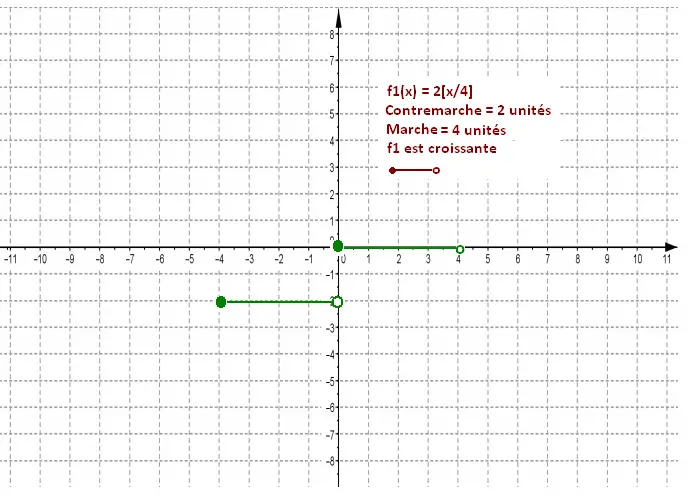
f1(x) = 2[x/4]
a = 2 : Contremarche = 2 unités
b = 1/4: Marche = 1/b = 4 unités
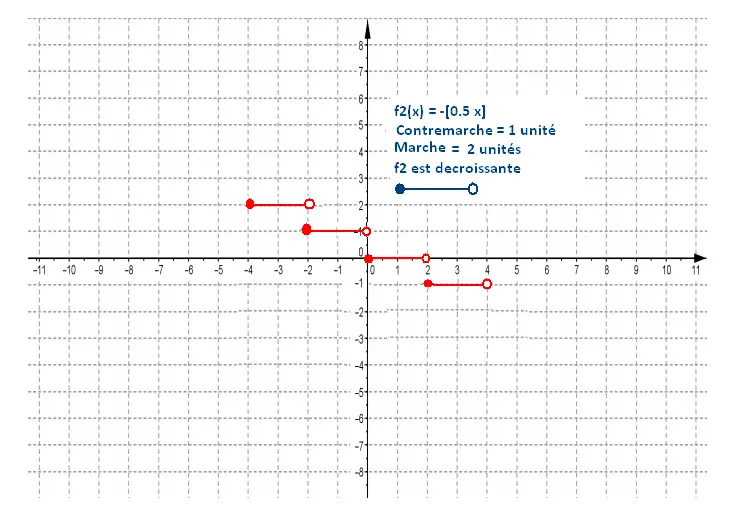
f2(x) = -[0.5 x]
a = - 1 : Contremarche = 1 unité
b = 0.5: Marche = 1/b = 2 unités
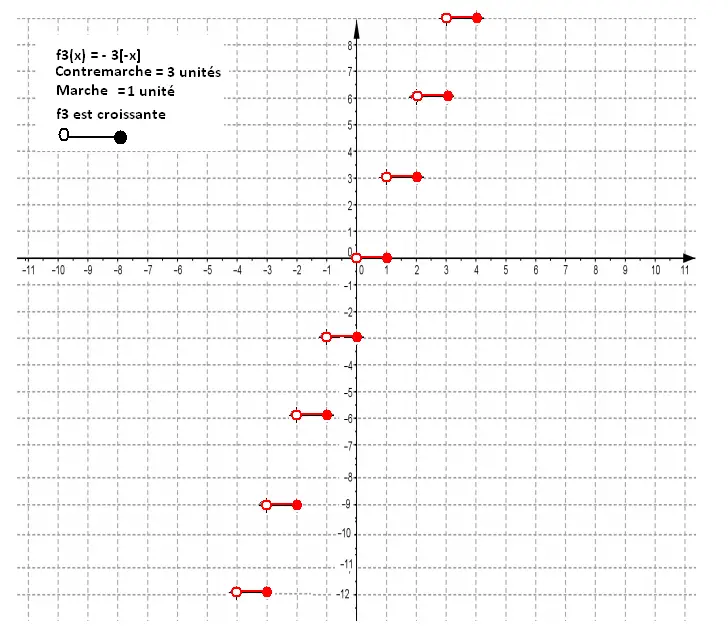
f3(x) = - 3[-x]
a = - 3 : Contremarche = 3 unités
b = - 1: Marche = 1/-1 = - 1 = 1 unité
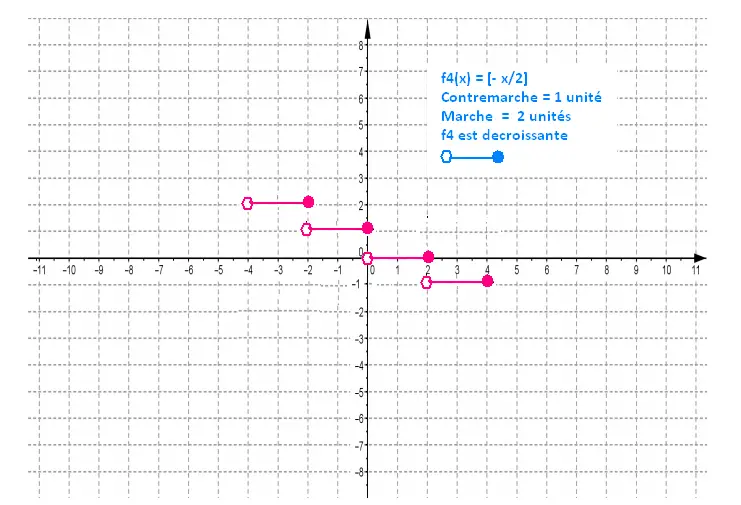
f4(x) = [- x/2]
a = 1 : Contremarche = 1 unité
b = - 1/2: Marche = 1/(-1/2) = - 2 = 2 unités
2) Variations des fonctions
f1(x) = 2[x/4]
a = 2
b = 1/4
a et b de même signe : f1 est croissante
f2(x) = -[0.5 x]
a = - 1
b = 0.5
a et b de signe contraire: f2 est decroissante
f3(x) = - 3[-x]
a = - 3
b = - 1
a et b de même signe : f3 est croissante
f4(x) = [- x/2]
a = 1
b = - 1/2
a et b de signe contraire: f4 est decroissante
3) Orientation des segments:
f1(x) = 2[x/4]
b = 1/4 > 0 : 
f2(x) = -[0.5 x]
b = 0.5 > 0 : 
f3(x) = - 3[-x]
b = - 1 < 0 : 
f4(x) = [- x/2]
b = - 1/2: < 0 : 
4) Graphique des fonctions
Exercice 2
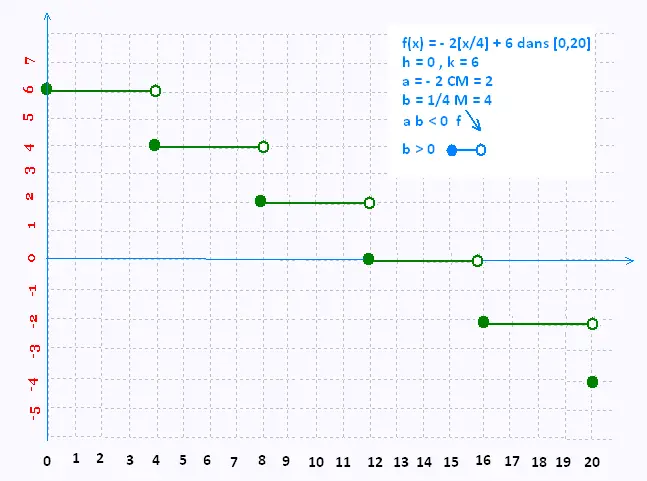
f(x) = - 2[x/4] + 6 dans [0,20]
a) Tableau de valeurs:
| x |
0 |
2 |
4 |
8 |
12 |
16 |
20 |
| y |
6 |
6 |
4 |
2 |
0 |
- 2 |
- 4 |
Graphique:
b)
1) L'image de la fonction est {- 4, - 2, 0, 2, 4, 6}
2) Minimum = - 4,
3) Maximum = 6
4)L'ensemble des zéros [12, 16 [
c) Cette fonction est décroissante, car a et b sont de signe contraire.
d) Cette fonction est positive dans [0, 12[. Elle est négative
dans [16, 20].
|
|







