Maths
- 2 -
Fonction en escalier
Fonction partie entière
Exercices
© The scientific sentence. 2010
| |
Mathématiques 2: Fonctions
Fonction en escalier
Fonction partie entière
Le plus grand entier inférieur ou égal.
1. Definitions
Une fonction en escalier est une fonction constante
sur des intervalles définis.
La fonction en escalier est une fonction étagée. Elle est
définie sur l’ensemble des réels et dont les valeurs (réelles) sont
constantes sur des intervalles.
On dit que cette fonction est constante par morceaux.
Un cas particulier de la fonction en esclaier est la
fonction « la partie entière ».
2. Partie entière d'un nombre réel
La partie entière d'un nombre réel
x est le grand entier
relatif n inférieur ou égal à x.
La fonction partie entière de la variable réelle x se note [x]
Exemples:
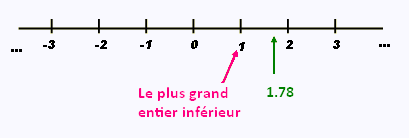
Si x = 1.78, alors [x] = 1. C'est le plus grand entier inférieur à 1.78.
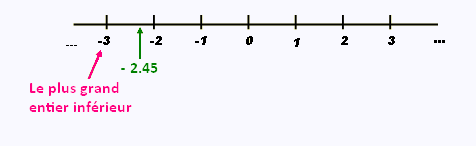
Si x = - 2.45, alors [x] = - 3. C'est le plus grand entier inférieur à - 2.45.
[0] = 0, [4.35] = 4, [- 0.5] = - 1.
La fonction partie entière sert à représenter des situations dans lesquelles la variable dépendante ne varie pas alors que la variable indépendante varie.
2. La fonction partie entière de base
Le modèle théorique de la fonction partie entière de base est
donné par le graphique suivant:
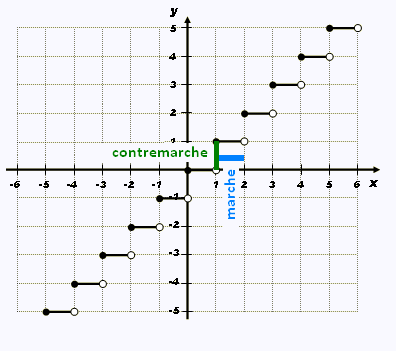
Ses aractéristiques sont:
• Les intervalles de valeurs de la variable indépendante sont fermés à gauche,
celà signifie que la première valeur de l’intervalle est incluse.
Par exemple [ 0 , 1 [ ou  . .
• La distance entre les marches est de 1 unité.
• L’ordonnée à l’origine est 0.
• Les abscisses à l’origine sont dans l’intervalle [ 0 , 1 [ .
• La fonction f , partie entière de x , qui associe à chaque nombre
réel x le plus grand entier inférieur ou égal à x est définie par f(x) = [ x ] ;
dom f = R et ima f = Z , c'est à dire la partie entière seulement.
{ … -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, … }
2. Forme canonique d'une fonction partie entière
La forme canonique d'une fonction partie entiere est la suivante:
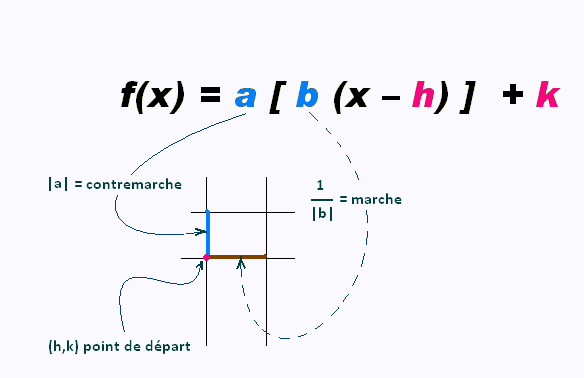
Les paramètres du point de départ h et k , ainsi que les
paramètre a et b sont fixés.
Le paramètre a est apppelé contremarche.
Le paramètre 1/|b| est appelée marche.
La fonction partie entière est un type de fonction en escalier.
Elle est distinguée par sa régularité .
Les marches ont toutes la même longueur.
La distance entre les marches est toujours la même.
Par contre, pour une fonction en escalier quelconque,
les marches ont des longueurs différentes, et
les distances entre les marches sont différentes.
|
|