Mathématiques 2: Algèbre
Partie entière

1. Definitions

La partie entière d’un nombre correspond au plus grand entier inférieur ou égal à ce nombre.; c'est à dire à l'entier qui le précède.

La partie entière d’un nombre x est notée [x].

Exemples:

[0] = 0; [2.0] = 2; [- 3.0] = - 3; [1.5] = 1; [0.5] = 0; [- 0.5] = - 1 ; [- 12.56] = - 13;

Le domaine de définition de la fonction partie entière est l'ensemble des réels R: dom = R. Son image est l'ensemble des entiers relatifs: codom = Z.

Son graphique correspond à celui d'une fonction en escalier.

Son expression générale est de la forme:

f(x) = a [b (x - h)] + k

Le coefficient "a" correspond au variation de f(x), c'est à dire a = Δy. Le coefficient "b" correspond à l'inverse de la variation de x; c'est à dire b = 1/Δx.

On appelle Δx la marche de la fonction; et Δy la contremarche de la fonction.

La fonction la plus simple est f(x) = [x]. Elle est appelé fonction de base

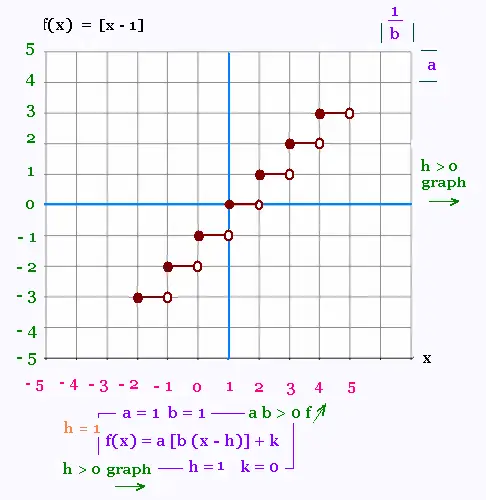
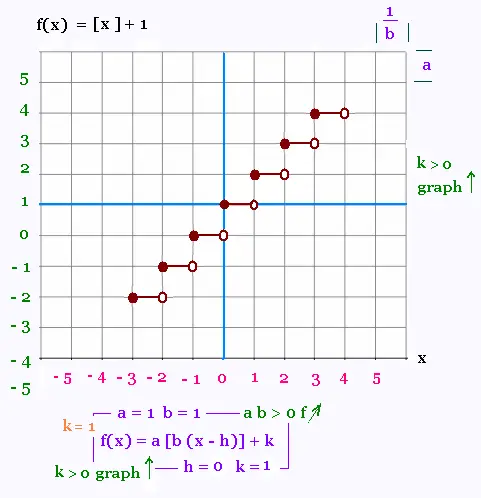
2. Représentations graphiques

Nous allons représenter les 4 cas possibles selon les signes des coefficients a et b, puis montrer comment le graph peut être glissé horizontalement selon la valeur de h et verticalement selon la valeur de k.

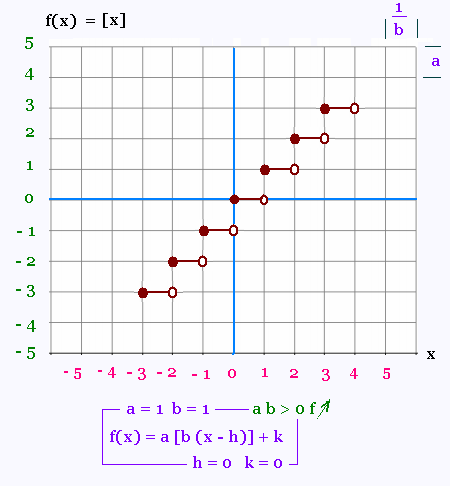
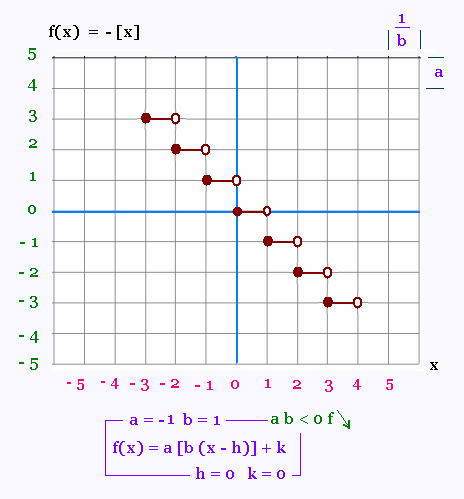
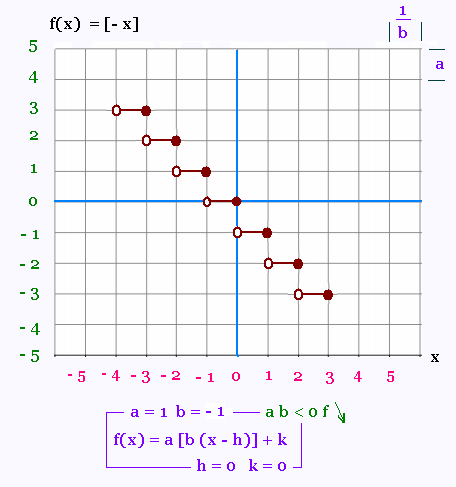
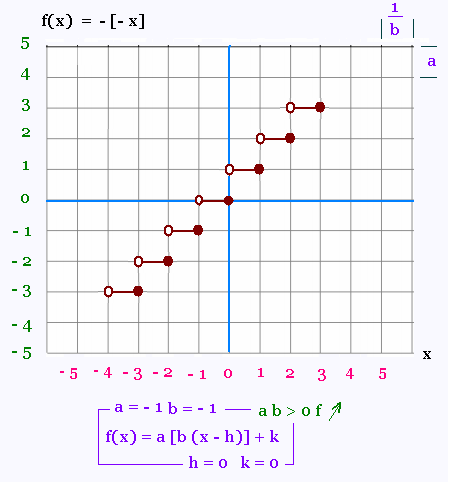
3. Exemples

1. Tracer le graphe d'une fonction
à partir de sa forme

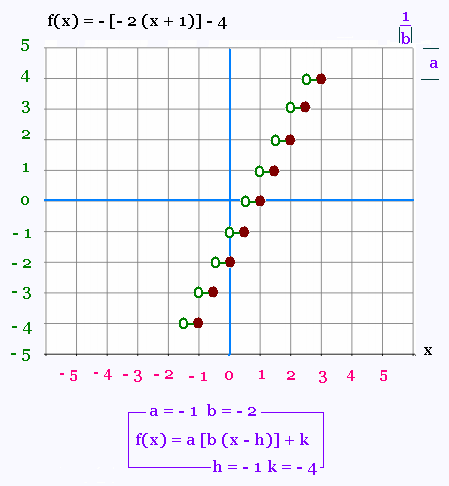
On veut tracer le graphique de la fonction suivante:

f(x) = - [- 2 x - 2] - 4

Il est utile tout d'abord de réecrire l'expression de la fonction en faisant apparaître les coefficients:

f(x) = - [- 2 (x + 1)] - 4

D'où: a = - 1, b = - 2, h = - 1, et k = - 4

Nous avons donc:

Marche = 1/|b| = 1/2 = 0.5
Contremarche = |a| = 1
h = - 1
k = - 4

a < 0, b < 0, donc la fonction est croissante.

b < 0, le segment est donc de la forme:
point-vide point-plein ∘-•.

Il suffit de commencer par un point, par exemple le poit (h, k) = (- 1, - 4) et de continuer de tracer les segments point-vide point-plein ∘-•.

2. Etablir la forme de la fonction
à partir de son graph

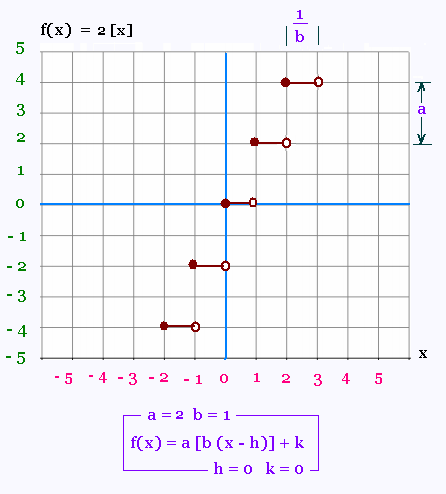
La marche est égale à 1/1 = 1. La contremarche est égale à Δy = 2 (par exemple f(2) - f(1) = 4 - 2 = 2)

Le point plein (h,k) le plus proche de O(0,0) est le point O(0,0). Donc h = 0 et k = 0.

Ainsi:

f(x) = 2[1(x - 0)] + 0 = 2 [x].

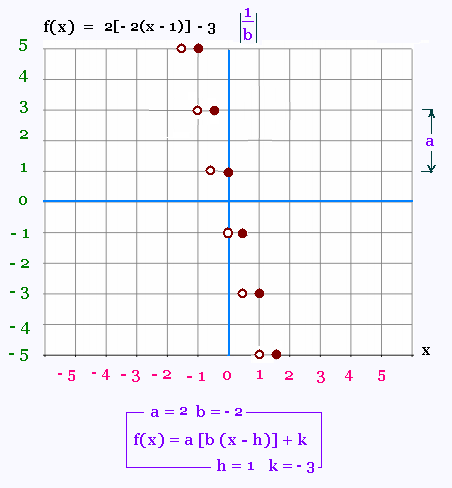
La marche est égale à 1/|b| = 1/2. La contremarche est égale à Δy = 2 (par exemple f(-1/2) - f(0) = 3 - 1 = 2)

Le point plein (h,k) le plus proche de O(0,0) est le point O(0,1). Donc h = 0 et k = 1.

On peut prendre le point plein (1, -3 ) qui donne les mêmes valeurs.

Ainsi:

f(x) = 2[- 2 x] + 1.
ou
f(x) = 2[- 2(x - 1)] - 3 .