Maths
- 2 -
Fonction en escalier
Fonction partie entière
Exercices
© The scientific sentence. 2010
| |
Mathématiques 2: Fonctions
Fonction partie entière
Propriétés
1. Propriétés de la fonction partie entière
• Propriété 1
Alors que la fonction en escalier est définie de R vers R;
la fonction partie entière est définie de R vers Z.
• Propriété 2:
[x] ≤ x < [x] + 1
Cette propriété est utile pour retrouver les valeurs de x quand
on connaît une valeur de f(x), c’est à dire résoudre l'équation
[x] = n où n est est donné.
2. Exemple
Comme pour toutes les fonctions, les propriétés de la fonction
partie entière sont ajustables selon le contexte considéré,
c’est-à-dire dans une situation réelle.
Voici un exemple:
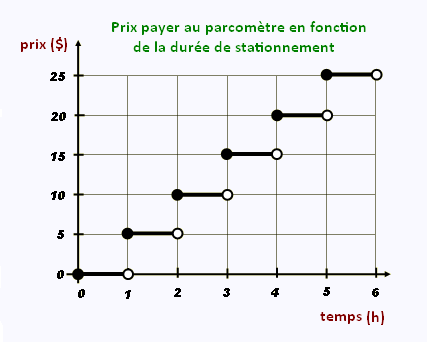
On doit payer, dans un parcomètre, la durée
de stationnement, gratuit la premièr heure,
selon le graphique ci-contre:
Analyse de la situation (fonction):
• Dom: [ 0, 6 [.
• Codom: { 0, 5, 10, 15, 20, 25 }
• La fonction est croissante dans [0, 6[
• f est positive dans [ 0, 6[
• f est négative dans aucun intervale
• Ordonnée à l'origine 0
• Abscisse à l'origine : tout l'intervale [ 0, 1[
• Extremum: maximum absolu: 25, minimum absolu : 0
3. Analys des propriétés
Dans la fonction partie entière:
f(x) = a [b(x - h)] + k
Les paramètres b et h sont reliés au domaine de la fonction.
Les paramètres a et k sont reliés au codomaine.
le terme partie entier est un entier N , on a donc:
f(x) = a N + k. Donc:
codom : { y ∈ R | y = aN + k, N ∈ Z }
1. Fonction partie entière de base
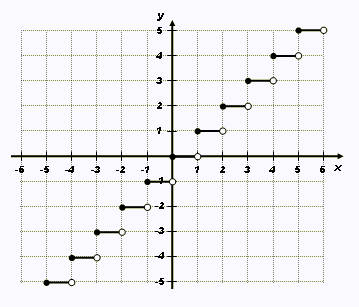
L'ensemble des marches (intervalles) représente tous les réels,
donc dom = R.
codom : Z : { … , - 5, - 4, - 3, - 2, - 1, 0, 1, 2, 3, 4, 5, … }.
Cette fonction ne retient que la partie entière des nombres,
donc que des entiers.
La fonction est croissante sur l'ensemble de son domaine.
f(x) ≥ 0 sur [0, + ∞[
f(x) < 0 sur ]- ∞, 0[
Ordonnée à l’origine f(0) = 0
Abscisses à l’origine f(x) = 0 : Tous les x ∈ [0 , 1[
Extrémum : aucun
2. Fonction partie entière transformée
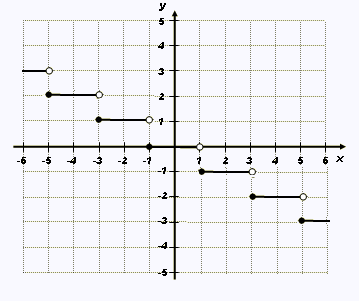
f(x) = - [0.5 (x + 1) ] + 0 = - [0.5 (x + 1) ]
Pour analyser une fonction partie entière, il est toujours
préférable de dessiner son graphique; quelques marches,
autour de l'origine, suffisent.
dom : R
codom y = - N + 0 = - N , N ∈ Z
ima : { … , - 4, - 3, - 2, - 1, 0, 1, 2, 3, 4, … } = Z
La fonction est decroissante dans
l'ensemble de son domaine R.
f(x) ≥ 0 dans ]- ∞ 1[
f(x) < 0 dans [1, + ∞[
Ordonnée à l’origine: f(0) = 0
Abscisses à l’origine: f(x) = 0 :
pour x ∈ [- 1, 1[
Extremum aucun
Il peut arriver qu’une fonction partie entière n’ait pas de zéro.
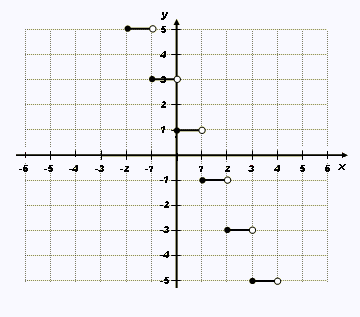
Généralement, dans la règle: f(x) = a [ b (x – h) ] + k, on a
- k/a = [ b (x – h) ]
• Si - k/a ∉ Z , il n’y a aucun zéro.
• Si - k/a ∈ Z , il y a une infinité de zéros.
Dans l'exemple: f(x) = - 3 [ x ] + 4
- k/a = -4/-3 = 4/3 ∉ Z , il n’y a aucun zéro.
Dans l'exemple: f(x) = - [ 3(x – 1) ] - 2
- k/a = 2/-1 = - 2 : &ixin; Z , il y a une infinité de zéros.
On remarque qu'à l'intérieur d'un intervalle, il y a une infinité de nombres,
donc une infinité de zéros.
2. Fonction partie entière dans un contexte donné
Les propriétés d’une fonction sont différentes lorsqu’elle
est en contexte, c’est-à-dire lorsque qu’on l’étudie en lien
avec une situation réelle considérée.
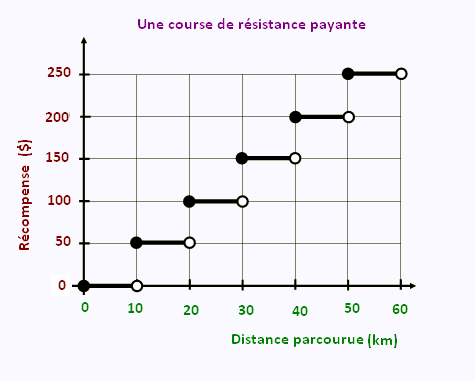
Dans une course à pieds de résistance non-stop de longeur 60 km, le coureur
est payé 50 $ pour chaque tranche de 10 km effectuée.
Analyse cette situation (fonction) sur [ 0, 60 [.
Dom = [0, 60 [
Codom = [ 0, 250[
f est croissante
f(x) ≥ 0 dans Dom
f(x) n'est pas négative dans ce contexte.
f(x) = 0 pour x ∈ [0, 10[
Extrémum maximum absolu : 250
minimum absolue: 0
|
|