Mathématiques 45: Algèbre:
Polynômes

Quand on effectue des opérations sur les polynômes, on distribue les termes, on applique les lois des exposants, et on simplifie.

Rappelons les règles suivantes:

1. x^ax^b = x^a+b
2. (x^a)^b = x^ab
3. (xy)^a = x^ay^a
4. (x/y)^a = x^a/y^a
5. x^-a = 1/x^a
6. x^a/x^b = x^a-b = 1/x^b-a
7. (x/y)^a = (y/x)^-a
8. x⁰ = 1 si x≠0

1. Multiplication des polynômes

Pour multiplier deux polynômes entre eux, on distribue les termes de l'un aux termes de l'autre, tout en applicant les règles des exposants.

Multiplier deux polynômes, c'est développer l'expression algébrique de leur produit.

(♣ + ♥)(♣ - ♥) = ♣² - ♣♥ + ♥♣ - ♥²

On simplifie toujours l'expression finale:

(♣ + ♥)(♣ - ♥) = ♣² - ♥²

Exemples

1. 4(x + 5) = (4)(x) + (4)(5) =
4x + 20

2. 3x(2x - 6) = (2x)(3x) - (3x)(6) =
6x² - 18x.

Attention au signe - !


3. 4x (2x + 3) – 5x (7x² + 2x) =
(4x)(2x) + (4x)(3) - (5x)(7x²) - (5x)(2x) =
8x² + 12x - 35x³ - 10 x²

On rassemble les termes semblables:
= 8x² - 10 x² - 35x³ + 12x =
- 2x² - 35x³ + 12x =
= - 35x³ - 2x² + 12x .


4. (2x + 3)(4x - 5) = (3x)(4x) - (3x)(5) + (3)(4x) - (3)(5) =
12x² - 15x +12x - 15 =
12x² - 3x - 15


5. (2x² + 3x + 1)(4x² - 5x - 4) =
(2x²)(4x²) - (2x²)(5x) - (2x²)(4) + (3x)(4x²) - (3x)(5x) - (3x)(4) + (1)(4x²) - (1)(5x) - (1)(4) =
8x⁴ - 10x³ - 8x² + 12x³ - 15x² - 12x + 4x² - 5x - 4 =
8x⁴ + 2x³ - 19x² - 17x - 4.

On range toujours les termes d'un polynôme
par ordre de degré décroissant.

2. Division des polynômes

2.1. Division d'un polynôme par un monôme

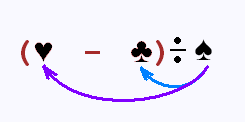
Comme pour la multiplication, la division d'un polynôme par un monôme se fait par distributivité.

Exemples:

1. (6x + 15)÷3 = 6x÷3 + 15÷3 =
2x + 5

2. (6x⁴ + 15x)÷3x = 6x⁴÷3x + 15x÷3x =
2x³ + 5

2.1. Division d'un polynôme par un polynôme

On peut diviser un polynôme par un autre. Une telle opération nécessite la condition que le degré du numérateur est plus grand que le degré du dénominateur.

La division se fait suivant la dite division Euclidienne:

dividende = (quotient x diviseur) + reste.

La règle est la suivante:

. On cherche la plus grande valeur qui, multipliée par le premier terme du diviseur donnera comme réponse le premier terme du dividende.

. On effectue la distributivité de la multiplication du teme trouvé sur le diviseur. On obtient un premier reste.

. On effectue la soustraction du dividende et du premier reste.

. On continuer ainsi jusqu'à ce que l'on obtient un reste de degré plus petit que celui du diviseur:

. Enfin, en ecrit le résulat sous forme d'une formule:

dividende = (quotient x diviseur) + reste .

Voici deux exemples, un sans reste et l'autre avec reste.

1. Sans reste:

Considérons les deux polynômes:
P(x) = x³ + 2 x² + 3x - 6, et
Q(x) = x - 1



x³ + 2x² + 3x - 6 = (x² + 3x + 6)(x - 1)


2. Avec reste:

P(x) = x³ + 2x² + 3x, et
Q(x) = x - 1



(x³ + 2x² + 3x) = (x² + 3x + 6)(x - 1) + 6