Maths
- 2 -
Avec
Geogebra
© The scientific sentence. 2010
|
Mathématiques 23 Géométrie
Droites remarquables dans un triangle
Les droites remarquables dans un
triange sont les médiatrices, les hauteurs, les
bissectrices, et les médianes.
Activité 1 : Médiatrices dans un triangle
1.1. Définition d'une médiatrice
La médiatrice d’un segment est la droite perpendiculaire à ce segment et qui passe par le milieu de ce segment.
C'est aussi l’axe de symétrie de ce segment.
1.2.Propriétés de la médiatrice
Propriété 1:
Si un point est sur la médiatrice d’un segment, alors il est à égal distance des deux extrémités de ce segment.
Propriété 2:
Si un point est à égale distance des deux extrémités d’un segment, alors il se trouve sur la médiatrice de ce segment.
1.3. Tracé d'une médiatrice
a) Sans utiliser l'outil médiatrice:
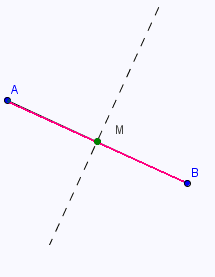
• Tracer un segment [A,B] avec l'outil
segment entre deux points.
• Placer le milieu du segment [A,B]
avec l'outil milieu ou centre.
• Tracer la perpendiculaire au segment [A,B]
avec l'outil perpendiculaire .
• cliquer sur le point C et le renommer
en M.
• Placer le point C qui n'est pas sur la droite (AB).
• Tracer les segments [AC] et [BC]. On obtient le
triangle ABC.
b) En utilisant l'outil médiatrice:
• Tracer le médiatrice de [AC]
• Nommer O le point d'intersection des deux médiatrices
construites.
• Tracer le médiatrice de [BC]
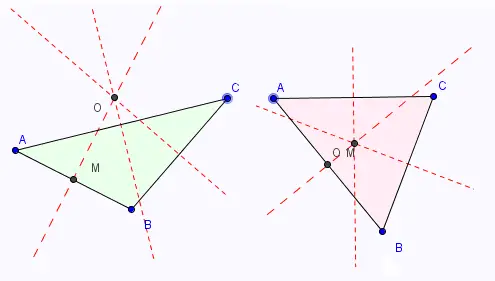
Les 3 médiatrices du triangle ABC sont concourantes en un point O.
En déplaçant les sommets A, B, et C du triangle, le point d'intersection O des trois médiatrices se trouve soit à l'extérieur, soit à l'intérieur du triangle.
Les trois médiatrices restent concourantes au point O .
• Tracer le cercle de centre O passant par le point A
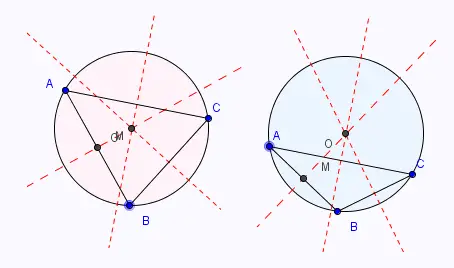
Les trois sommets A, B, et C du triangles se situent
sur le cercle.
Le cercle est appelé cercle circonscrit au triangle .
Propriété:
Les trois médiatrices des côtés d’un triangle sont concourantes au centre du cercle circonstrit à ce triangle.
Activité 2 : Hauteurs d' un triangle
2.1.Définition d'une hauteur
Une hauteur dans un triangle est la droite passant par un sommet et perpendiculaire au côté opposé à ce sommet.
2.2.Tracé d'une hauteur
• Tracer un triangle ABC.
• Tracer la droite D1 passant par A et
perpendiculaire à (BC).
La droite D1 est la hauteur du triangle passant
par A et perpendiculaire au côté [BC].
• Tracer la droite D2 passant par B et
perpendiculaire à (AC).
Soit H le point d'intersection des deux droites D1 et D2.
• Tracer la droite D3 passant par C et
perpendiculaire à (AB).
Utiliser l'outil renommer pour nommer
d1, d2 et d3 les trois hauteurs
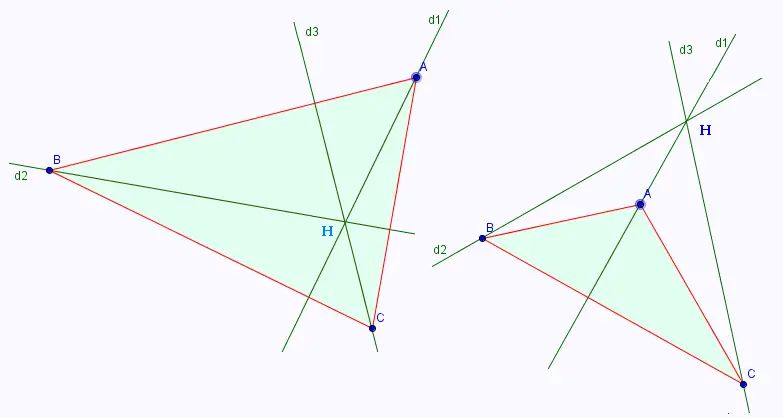
En déplaçant les sommets A, B, et C du triangle, le point d'intersection H des trois hauteurs se trouve soit à l'extérieur, soit à l'intérieur du triangle.
Les trois hauteurs restent concourantes au point O. Le point
O est appelé orthocentre du triangle ABC.
Activité 3 : Bissectrices des angles d'un triangle
3.1.Définition d'une bissectrice
La bissectrice d'un angle est la droite qui passe par le sommet de cet angle et qui partage cet angle en deux angles de même mesure.
3.2. Tracé d'une bissectrice
• Tracer un triangle ABC.
• Tracer les bissectrices des angles A, B et C.
I est leur point d'intersection.
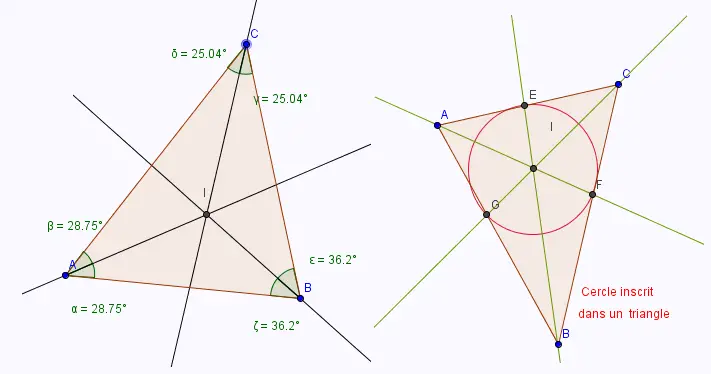
En déplaçant les sommets A, B, et C du triangle, le point d'intersection I des trois bissectrices reste toujours à l'intérieur du triangle.
Les trois bissectrices restent concourantes au point I. Le point I est appelé centre du cercle inscrit au triangle.
Activité 4 : Médianes d'un triangle
4.1.Définition d'une médiane
Une médiane d'un triangle est la droite qui joint un
sommet au milieu du côté opposé.
4.2.Tracé d'une médiane
• Tracer un triangle ABC.
• Placer les points I, J et K milieux respectifs des
segments [AB], [BC], et [AC]
• Tracer la droite (CI). Cette droite est
la médiane issue du point C.
• Tracer la droite (BK). Cette droite est
la médiane issue du point B.
• Nommer G le point d'intersection des droites
(CI) et (BJ).
• Tracer la droite (AJ). Cette droite est
la médiane issue du point A.
En déplaçant les sommets A, B, et C du triangle, le point d'intersection
G des trois médianes reste toujours à l'intérieur du triangle.
G est appelé centre de gravité du triangle.
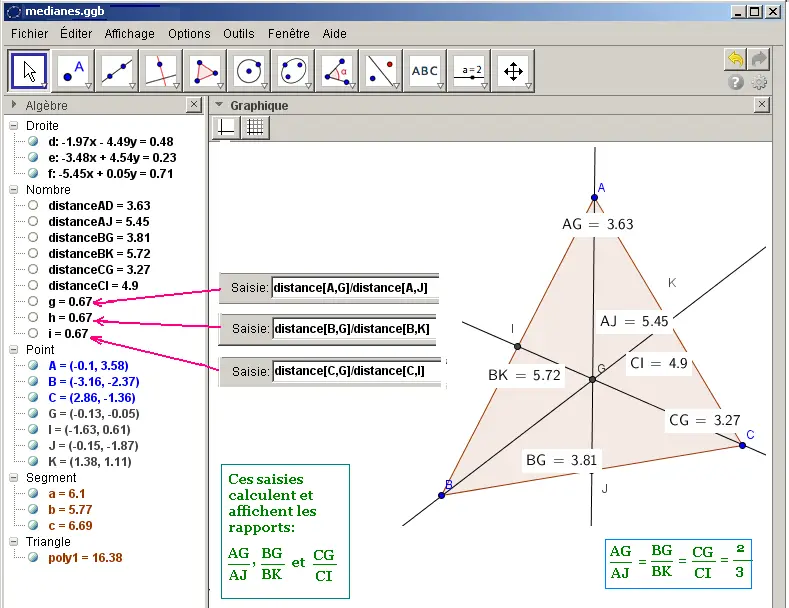
• Faire afficher les mesures des AG, AJ, BG, BK, CG, et CI.
• Faire calculer AG/AJ, BG/BK et CG/CI.
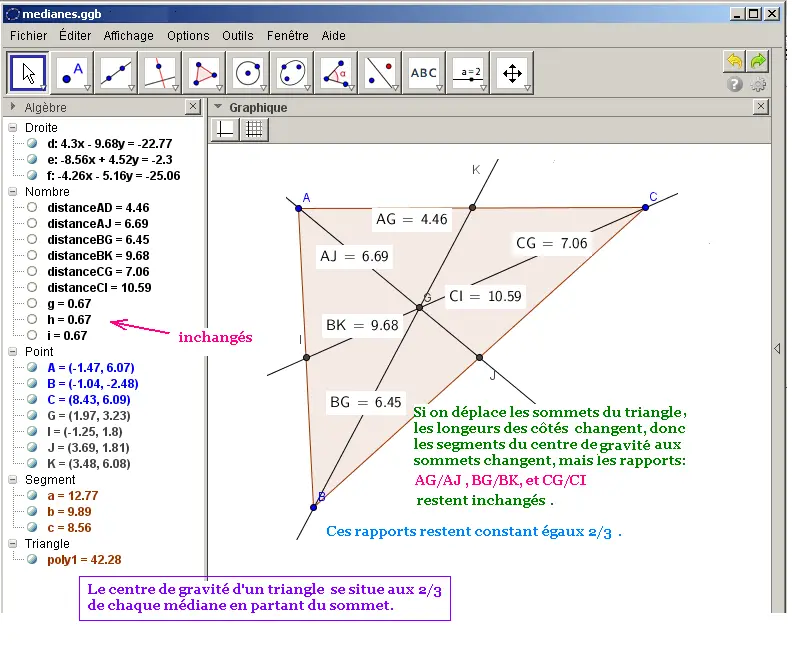
En déplaçant les sommets A, B, et C du triangle, toutes les mesures
changent sauf les trois rapports AG/AJ, BG/BK et CG/CI qui restent égaux à 0,67 = 2/3.
Le centre de gravité d'un triangle se situe aux 2/3 de chaque médiane en partant du sommet.
|
|