Maths
- 2 -
Avec
Geogebra
© The scientific sentence. 2010
|
Mathématiques 23 Géométrie
Théorème de Thalès avec Geogebra
1. Théorème de Thalès: configuration triangle
Conjecture = énoncé qui semble vrai alors qu’on ne l’a pas encore prouvé.
1.1. Activité 1:
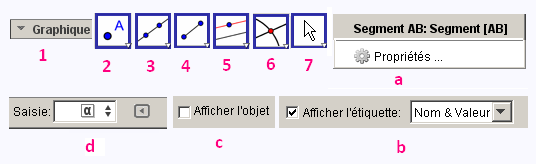
• Lancer le logiciel GeoGebra,
• Cliquer su Graphique et désactiver les axes (outil 1),
• Placer trois points non alignés A, B et C sur l’espace de travail (fenêtre de droite) (outil 2),
• Tracer les droites (AB) et (AC) (outil 3),
• Tracer les segments [AB], [AC] et [BC] (outil 4),
• Pour le segment [AB] : cliquer droit sur le segment [AB],
sélectionner Segment [AB], puis Propriétés et ensuite
afficher l’étiquette : Sélectionnons "Nom & Valeur" (outils a et b),
• Reproduire la procédure pour chacun des deux autres
segments [AC] et [BC],
• Plaçons le point N sur la droite (AC) (outil 2),
• Tracer la droite parallèle au segment [CB] passant par le point N (outil 5),
• Placer le point M intersection des droites (AB) et (NM) (outil 6),
• Tracer les segments [AN][AM] et [MN] (outil 4),
• Pour le segment [AN] : cliquer droit sur le segment [AN],
sélectionnons segment [AN], puis Propriétés et ensuite
afficher l’étiquette : Sélectionner "Nom & Valeur" (outils a et b),
• Reproduire cette procédure pour chacun des deux autres
segments [AM] et [MN],
• Cliquer droit sur la droite (MN), sélectier "Droite MN",
puis décocher "Afficher l’objet" (outil c),
• saisir les rapports AM/AB, AN/AC, et MN/BC (outil d),
• On obtient la figure suivante:
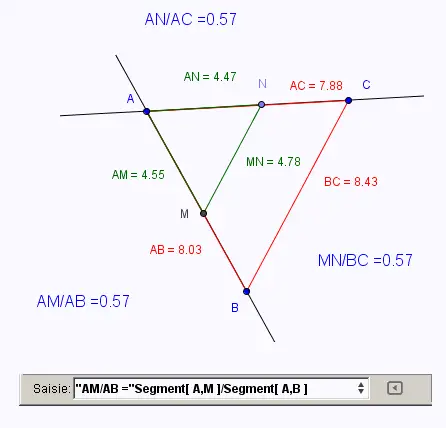
1.2. Activité 2:
Déplacer le point B ou C ou le segment BC.
Déplacer le point A ou B ou le segment AB .
Déplacer le point A ou C ou le segment AC.
On constate que les rapports de Thalès restent fixes.
Déplacer le point N.
On constate que les rapports de Thalès restent égaux entre eux.
Conclusion:
Dans un triangle ABC,
si M est un point du côté [AB], N un point du côté [AC],
et si les droites (BC) et (MN) sont parallèles,
alors :
Ceci constitue le théorème de Thalès.
2. Exercice: Théorème de Thalès: configuration triangle
On utlisera les outils siuivants:

• Construire un triangle ABC,
• Tracer les droites (AB) et (AC)
• Placer un point sur la droite (AB) (mais pas sur le segment [AB]),
Renomme ce nouveau point M (fais un clic droit sur le point et choisis "Renommer"),
• Tracer la parallèle à (BC) passant par M,
• Placer un point à l’intersection de la parallèle et de (AC). Appeller ce point N,
• Déplacer le point M pour qu’il soit sur le segment [AB],
• Afficher la valeur de AM/AB dans la fenêtre "Saisie" (en bas) taper précisément: "AM/AB="distance[A,M]/distance[A,B],
suivie d’entrée. Déplacer le texte qui s’affiche,
• Afficher la valeur de AN/AC: tape dans "Saisie"(en bas):
"AN/AC= "distance[A,N]/distance[A,C] ,
• Afficher la valeur de MN/BC : tape dans "Saisie" (en bas):
"MN/BC="distance[M,N]/distance[B,C],
• On obtient la figure suivante:
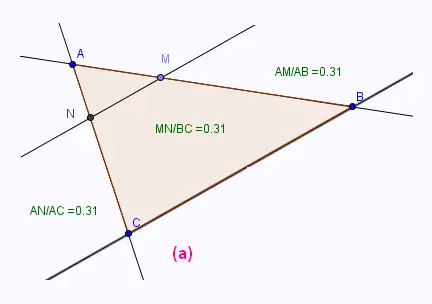
Remarquer que lorsque M se déplace sur [AB], les trois rapports
ont tous le même valeur.
Conclusion:
Dans un triangle ABC,
si M est un point quelconque du côté [AB], N un point quelcnque du côté [AC],
et si les droites (BC) et (MN) sont parallèles,
alors :
Ceci constitue le théorème de Thalès.
3. Exercice: Théorème de Thalès: configuration papillon
• Déplacer le point M de sorte qu’il ne soit pas sur [AB)
On obtient la configuration dite configuration de Thalès en papillon.
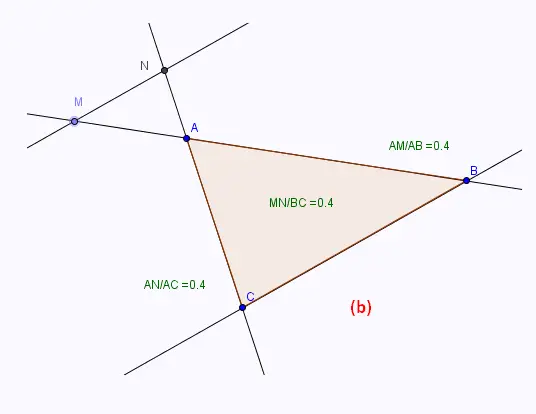
• Déplacer le point M, en gardant cette configuration, on remarque que les trois rapports ont tous le même valeur.
• Construire le point M’ symétrique de M par rapport à A,
• Construire le point N’ symétrique de N par rapport à A,
• Tracer la droite (M’N’),
• M’ est le symétrique de M par rapport à A et N’ est
le symétrique de N par rapport à A.
On a donc AM = AM’, AN = AN’, MN = M'N' et (MN)// (M'N') .
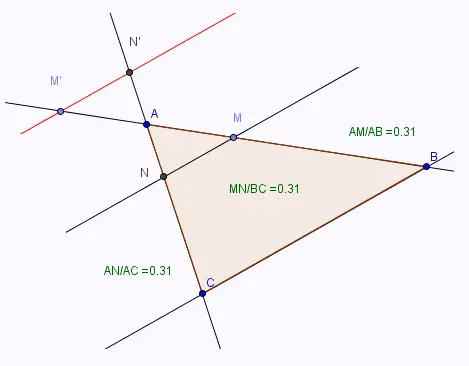
• Déplacer le point M, pour passer d'une configuration, à une
autre:
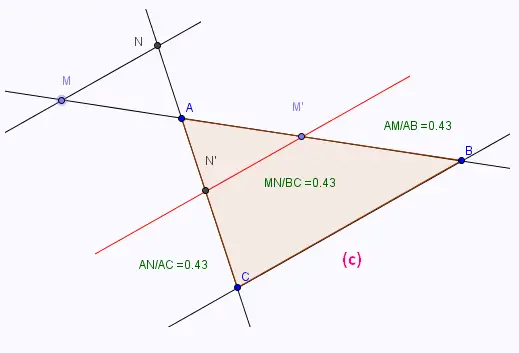
On a donc:
• En déduire:
Soient (AB) et (AC) deux droites sécantes en A,
Soient B et M deux points de la droite (AB), distincts de A,
Soient C et N deux points de la droite (AC), distincts de A.
Si les droites (BC) et (MN) sont parallèles, alors :
Ceci constitue le théorème de Thalès.
4. Exercice: Réciproque du théorème de Thalès
Objectif : Conjecturer la réciproque du théorème de Thalès.
1. Construire deux droites (MB) et (NC) sécantes.
2. Placer le point d’intersection des deux droites. Nommer ce point A.
3. Tracer les segments [MN] et [BC].
4. Afficher les longueurs de AM, AB, AN et AC.
5. Afficher les rapports AM/AB et AN/AC
6. Grâce à l’outil "déplacer", On peut déplacer les points M, B, C et N.
Déplacer ces points afin que AM/AB = AN/AC (on peutdéplacer les droites aussi),
7. On constate que
lorsque AM/AB = AN/AC, les droites (MN) et (BC) sont parallèles.
Lorsque
, les droites (MN) et (BC) sont parallèles.
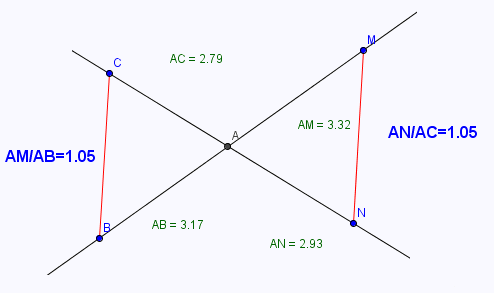
8. En plaçant le point N sur la demi-droit [A,C) en dehors du segment [A,C], on obtient la figure suivante:
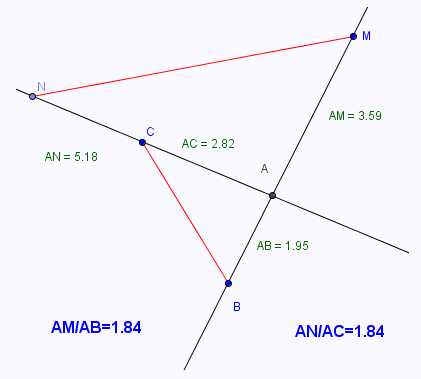
On remarque que même si les rapports sont égaux, les droites (MN) et (BC) ne sont pas parallèles.
Il faut préciser:
Les points A, M, B et les points A, N, C doivent être alignés dans le même ordre.
Finalement:
Si ,
Et si les points A, B, M sont dans le même ordre que les points A, C, N,
alors les droites (BC) et (MN) sont parallèles.
Ceci constitue la réciproque du théorème de Thalès.
|
|