Mathématiques 2: Les angles
1. Angles: définitions
1.1. Angle
Un angle est une figure géométrique limitée
par deux demi-droites qui se rencontrent en un point
commun. Les deux dem-droites sont les côtés de l’angle ;
le point commun est le sommet de l'angle.
On designe un angle par une lettre ciconflexe
comme ê ou par trois lettres ABC avec un circonflexe sur
la lettre du milieu. ici c'est B. On le designe aussi
par le symbol ∠B.
L’unité d’angle est le degré représenté
par °; ou le radian. On defini les angles selon
leur mesures.
Selon leur mesure, les angles
sont définis ainsi.
1.2. Angle nul
L'angle nul est un angle qui mesure 0 degré.
Ses deux côtés sont superposés.
1.3. Angle aigu
L'angle aigu est un angle qui mesure plus
que 0°, mais moins que 90°
1.4. Angle droit
L'angle droit est un angle qui mesure 90°
Ses deux côtés sont perpendiculaires l’un à l’autre.
1.5. Angle obtus
L'angle obtu est un angle dont la
mesure est comprise entre 90 et 180 degrés.
1.6. Angle saillant
L'angle saillant est un angle dont la
mesure est comprise entre 0 et 180 degrés.
1.7. Angle plat
Angle plat
Angle dont la mesure est de 180 degrés.
L'angle plat est un angle qui mesure 180 degrés.
Ses deux côtés forment deux demi-droites opposées
à partir du soomet de ll,angle. Le sommet est sur une même droite.
1.8. Angle rentrant
L'angle rentrant est un angle dont la
mesure est comprise entre 180 et 360 degrés.
1.9. Angle plein
L'angle plein est un angle qui
mesure 360 degrés.
2. Comparaison de deux angles
2.1. Angles congrus
Deux angles sont congrus lorsqu’ils ont la même mesure.
2.2. Angles complémentaires
Deux angles sont complémentaires lorsque
la somme de leurs mesures est égale à 90 degrés.
Le complément d’un angle est l'angle qui le complète
pour avoir un angle droit.
2.3. Angles supplémentaires
Deux angles sont supplémentaires lorsque
la somme de leurs mesures est égale à 180 degrés.
Le supplément d’un angle est l'angle qui le supplémente
pour avoir un angle plat.
2.4. Angles opposés par le sommet
Deux angles sont opposés par le sommet se
trouvent de part et
d'autre du point d'intersection de deux droites.
Deux angles sont opposés par le sommet sont congrus.
C'est à dire leurs mesures sont égales.
2.5. Angles adjacents
Deux angles sont adjacents lorsqu'ils ont
un point commun et sont situés de part et d’autre d’un
côté commun. Ils ont un même sommet et ils sont voisins
l'aun de l'autre.
2.6. Côtés adjacents
Un angle est formé par ces deux côtés qui lui ont adjacents.
Adjacent signifie voisin immédiat. Dans un angle , les
côtés [A,B] [A,C] sont adjacents à cet angle.
Dans un triangle rectangle, le côté le plus grand porte le
nom d'hyppoténuse. Par conséquent, un angle aigus dans ce triangle
possède un côté opposé et un côté adjacent. Donc trois noms
différents relatifs à chaque angle.
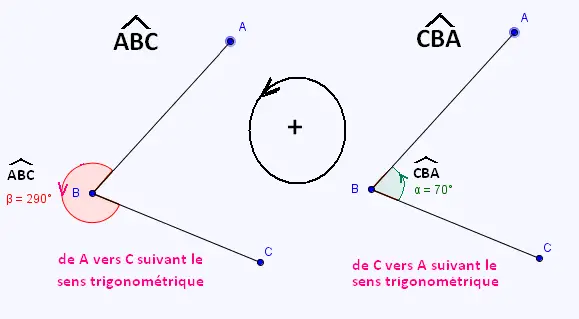
2.7. Orientations des angles
Un angle s'obtient en
tournant dans le sens trigonométrique, la demi-droite [BA) autour du
sommet B pour obtenir la demi-droite [BC).
Les angles et
sont différents.
L'un est saillant, l'autre est rentrant.
le sens trigonométrique est le sens inverse à celui des aiguilles
d'une montre.
|