Mathématiques:
Angles et arcs
1. Définitions
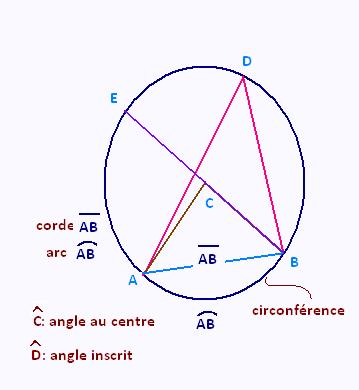 L' angle inscrit et
l'angle au centre
interceptent le même arc .
L' angle inscrit et
l'angle au centre
interceptent le même arc .
Nous avons CA = CB = rayon de la cercle de centre C
qui est égal à la moitié du diamètre BE .
La circonférence mesure 2 π x rayon = π x diamètre.
Un secteur est la zone délimitée par deux rayons et un arc compris entre
ces deux rayons, est. Un segment est la zone délimitée par une corde et
un arc.
Comment définir un radian?
Par définition, un radian est la mesure d'un angle
au centre d'un cercle interceptant un arc de longueur égale au rayon
du cercle.
La circonférence "C" d'un cercle de rayon R mesure 2πR. Nous avons
alors 2πR/R = 2π = 6.28 arcs meausurant R le long de la circonférence.
Si 180 degrés correspond à π radians, un radian = 180/π = 57.29 degrés .
Nous écrivons 1 rad = 57.29 o .
Le rad est utilisé dans les unités SI (Système international d'unités).
2. Angle inscrit et angle au centre
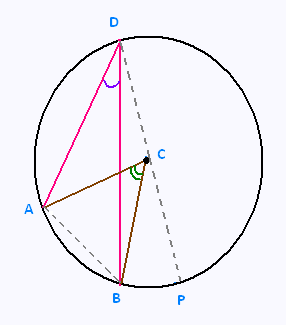
Le triangle ACB est isocèle puisque
AC = CB (rayons d'un même cercle). D'où
Le triangle ACD est isocèle puisque
AC = CD (rayons d'un même cercle). D'où
Le triangle BCD est isocèle puisque
CB = CD (rayons d'un même cercle).
D'où :
Nous avons
(R)
D'après la relation (R), on a:
Donc
Un angle inscrit est la moitié de
l'angle au centre qui intercepte le même arc.
3. Angle inscrit limite
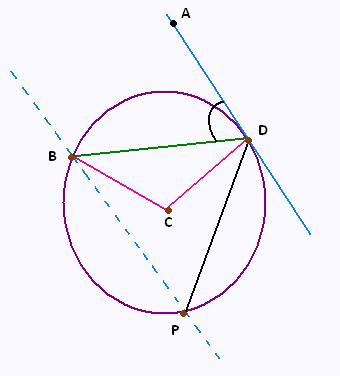
Le cas limite où l'angle inscrit est
formé par une corde et une tangente:
L'angle intercepte l'arc
<
(BP) parallèle à (DA):
Un angle inscrit est la moitié de la
angle au centre qui intercepter le même arc; même
dans le cas limite où l'angle inscrit est formé
par une tangente et une corde.
4. Deux cordes concourantes:
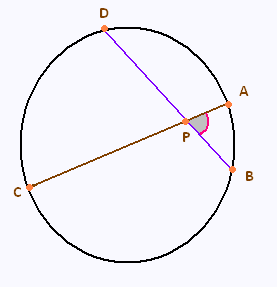
Soit deux cordes
Nous avons
5. Angle de deux sécantes:
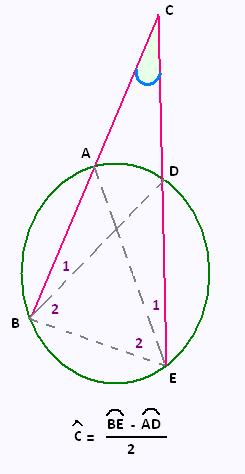
Deux sécantes (CB) et (CE) coupent un cercle.
D'où
• Cas particulier 1 :
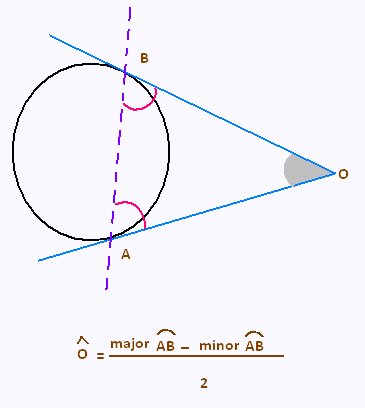
Deux droites tangentes au cercle.
Conséquences:
Le triangle AOB est isocèle.
• Cas particulier 2 :
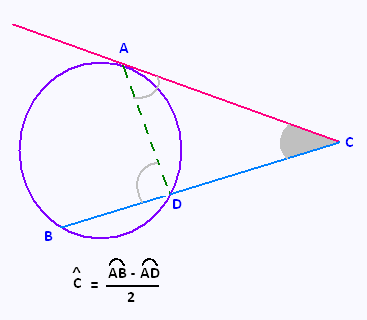
Une sécante et une tangente au cercle.
6. Exercice résolu
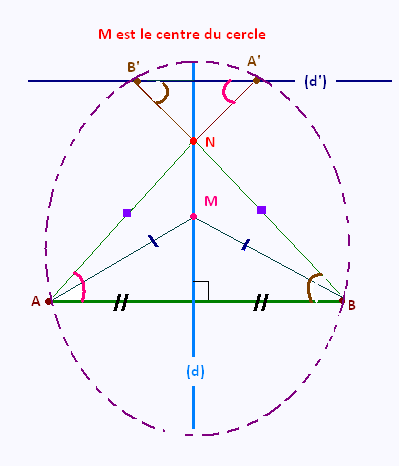
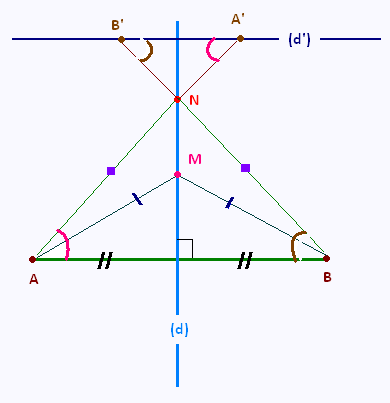
Soit un cercle de centre M. Sur ce cercle, on trace deux droites parallèles (AB) et (A'B') et deux sécantes (AA') et (BB') qui se coupent en N.
a) Montrer que le triangle A'NB' est isocèle.
b) Montrer que la droite (MN) est perpendiculaire à
à la droite (A'B').
a)
mes(A) = mes(A'): angles alternes internes.
mes(B) = mes(B'): angles alternes internes.
L'angle A intercepte l'arc A'B.
L'angle A' intercepte l'arc AB'
Donc les arc A'B et AB' sont isométriques.
L'angle B' intercepte l'arc A'B.
L'angle A' intercepte l'arc AB'
Les angles A' et B' interceptent des arcs isométriques,
D'après la propriété:
Deux angles inscrits qui interceptent le même arc ou des
arcs isométriques sont isométriques.
Donc mes (A') = mes (B') : le triangle A'NB'
est isocèle.
b)
Une même démonstration conduit au fait que
le triangle ANB est aussi isocèle.
ANB est isocèle, donc son sommet N est sur la médiatrice
de la base [AB].
M est le centre du cercle. Il est donc équidistant
des points A et B qui sont sur ce cercle. M est donc
sur la médiatrice du segment [AB]
Les points M et N sont tous les deux sur la médiatice
du segment [AB]. Ils sont donc alignés. Donc
la droite (MN) est perpendiculaire à (AB)
La droite (A'B') et (AB) sont parallèles. Toute
perpendiculaire à l'une est perpendiculaire à l'autre,
donc la droite (MN) est perpendiculaire à la droite
(A'B').
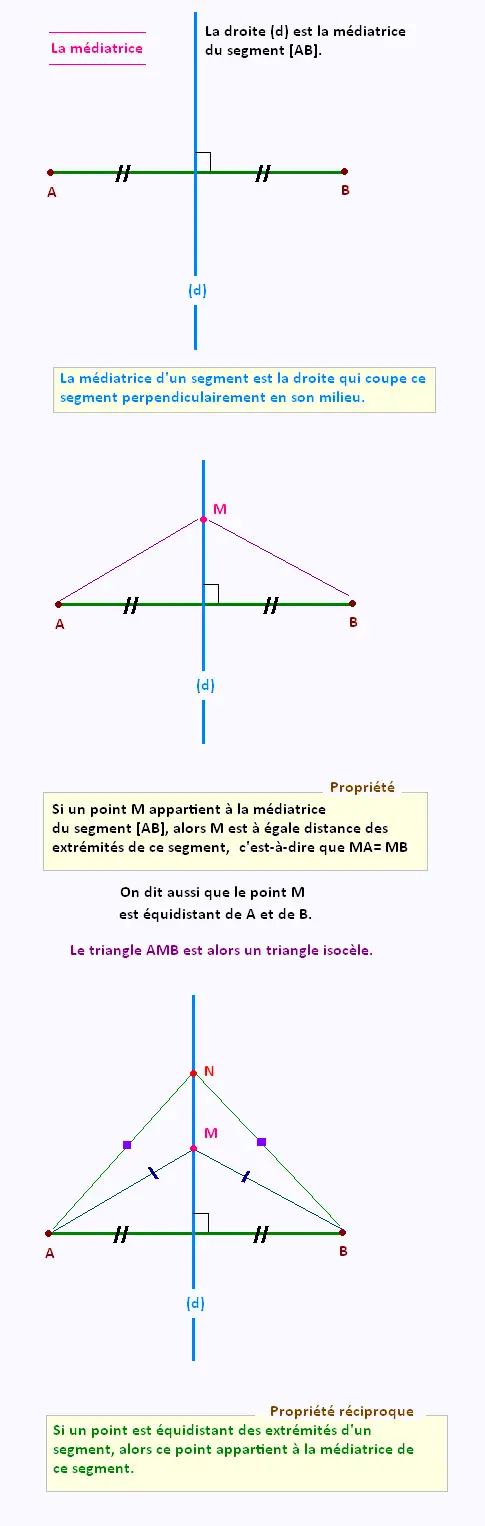
Rappels sur la médiatrice
d'un segment
|