Mathématiques 2: Cercle, disques et corps ronds
1. Cercle et circonférence
1.1. Definitions
Cercle:
Un cercle est une ligne fermée où tous
les points sont à égale distance d’un même
point appelé le centre.
Rayon:
Un rayon est le segment qui reliant
un point quelconque du cercle au centre du
cercle.
Diamètre:
Un diamètre est le segment qui relie
deux points du cercle et passant par le
centre.
Le diamètre est le double du rayon.
Si d est le diamètre du cercle et r son rayom,
alors
d = 2 x r et r = d/2
.
Corde :
Une corde est un segment qui relie deux
points quelconques d’un cercle.
Le diamètre est la plus longue corde du cercle.
Arc de cercle:
Un arc de cercle est une portion de cercle
délimitée par deux points qui forment une corde.
Angle au centre:
Un Angle au centre est l'angle
formé par deux rayons. Le sommet de l’angle
correspond donc au centre du cercle.
Relation entre le rayon et le diamètre:
Un diamètre est égal au double du rayon.
D = 2 x R ou R = D/2
D est le diamètre , R est le rayon
Circonférence:
La circonférence est la longueur du
contour d’un cercle ou le périmètre d’un cercle.
On calcule la circonférence à partir du diamètre
du cercle ou à partir de son rayon.
C = π x D ou C = 2πR
La valeur de π est égale à 3.1416
Cercle passant par trois
points non alignés:
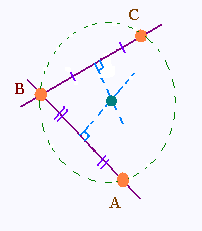 Soient 3 points non alignés A, B et C.
Soient 3 points non alignés A, B et C.
On joint les points A et B, puis B et C.
Le point des rencontre des médiatrices des segments
construits est le centre du cercle qui
passent par les 3 points.
Mesure d’un arc de cercle:
On mesure un arc de cercle de deux façons:
a) En degré. Sa mesure est égale à
celle de l’angle au centre qui intercepte cet arc.
b) En unités de longueur. On calcule
cette mesure à l'aide de la correspondance suivante:
Circonférence du cercle → 360°
Longueur de l'arc en unités de longueur → Mesure de
l'angle au centre qui intercepte cet arc en °.
Donc:
Longueur de l'arc =
(Mesure de l'angle au centre qui intercepte cet arc)x
(Circonférence du cercle)/360
2. Disque et secteur
Disque
Un disque est une surface plane délimitée
par un cercle. Son aire est égale à πr2.
Aire du disque = πr2
Secteur
Un secteur est une portion de disque délimitée
par deux rayons.
Son aire est égale à:
Aire du secteur =
(Mesure de l'angle au centre du secteur en°)x
(Aire totale du disque)/360°
3. Corps ronds et cylindre
| famille des solides |
| polyèdres | corps ronds |
| solide limité par des faces planes qui sont des
polygones.
|
Solide limité par au moins une face courbe
|
| prismes | pyramides |
cylindre | cône | sphère |
Cylindre droit
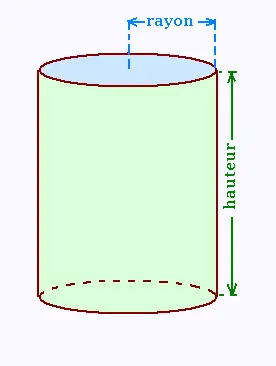
L'aire totale d'un cylindre droit est égale à
la somme des aires des deux disques (bases) et
celle du rectangle (surface latérale).
Son aire est égale à:
Aire totale du cylindre = Aire des deux bases + aire
latérale
Aire totale du cylindre =
2 x πr2 + 2 π r x h
r est le rayon h est la hauteur
Cône de révolution
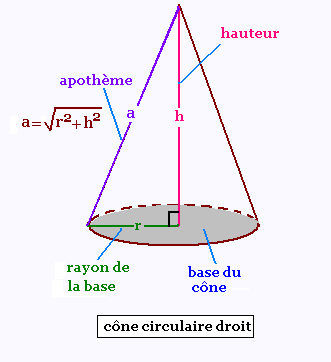
La base d'une pyramide est un polygone. La base d'un cône est
un cercle. La pyramide possède un apex, le
cône possède un sommet.
Un cône circulaire est un solide délimité par un disque circulaire qui est
sa base et une surface conique qui est sa surface latérale.
Dans un cône circulaire droit, la distance entre le
sommet et la base est perpendiculaire à cette base et passe par le centre
de cette base circulaire. Cette distance est la hauteur du cône.
Un cône circulaire droit est appelé cône de révolution.
Dans un cône circulaire droit, la distance entre le sommet du cône
et un point quelconque du cercle est constante et s'appelle l'apothème du cône.
L'aire totale d'un cône de révolution est égale à la somme de
l'aire de la base (πr2)et de celle de la surface
latérale (π r a).
L'aire totale d'un cône de révolution de rayon de base r, de
hauteur h et d'apothème a est égale à :
πr2 + π r a = πr(r + a)
a = √(r2 + h2)
Aire totale du cône de révolution =
πr2 + π r a = πr(r + a)
a = √(r2 + h2)
Sphère

L'aire d'une sphère de rayon r est
égale à 4πr2
Aire d'une sphère =
4πr2
r est le rayon de la sphère.
4. Exercices
Exercice 1: Applications
Determiner la circonférence du cercle si;
a) r = 4 cm
b) D = 3 m
c) Un angle au centre de mesure 60° intercepte
un arc de 4 cm.
Solution
a) C = 2 π r = 2 x π x 4 = 25.13 cm
b) C = π D = π x 3 m = 9.42 m
c) 60° → 4 cm
Donc 360° → 360° x 4 cm /60° = 24 cm.
Exercice 2: Croissant de lune
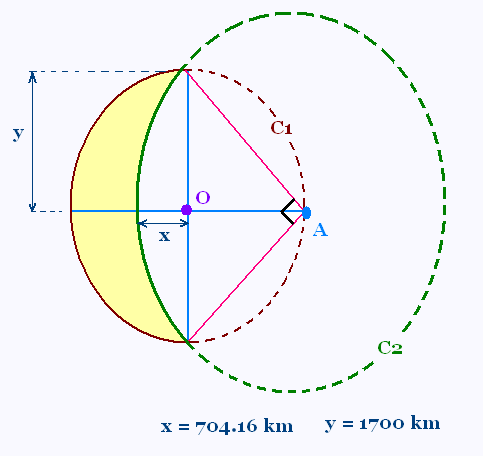
Un croissant de lune est formé de deux arcs
des cercles C1 de centre O et C2 de
centre A.
a) Quel est le périmètre du croissant?
b) Quel est l'aire du croissant?
Solution
a) Soient R1 et R2 les rayons des cercles C1 et C2
respectivement.
Nous avons:
R1 = y = 1700 km
R2 = R1 + x = y + x = 1700 + 704.16 = 2404.16 km.
Les circonférences respectives sont :
Γ1 = 2πR1 = 2 x 3.1416 x 1700 = 10681.41 km
Γ2 = 2πR2 = 2 x 3.1416 x 2404.16 = 15105.78 km
L'arc de cercle C1 intercepte un angle plat:
(arc de cercle C1)/Γ1 = 180°/360° = 1/2
(arc de cercle C1) = Γ1/2 = 10681.41/2 = 5340.70 km
L'arc de cercle C2 intercepte un angle droit:
(arc de cercle C2)/Γ2 = 90°/360° = 1/4
(arc de cercle C2)= Γ2/4 = 15105.78/4 = 3776.44 km.
Le périmètre du croissant est égal à : (arc de cercle C1) +
(arc de cercle C2) = 5340.70 + 3776.44 = 9117.14 km.
Le périmètre du croissant de lune est égal à 9117.14 km.
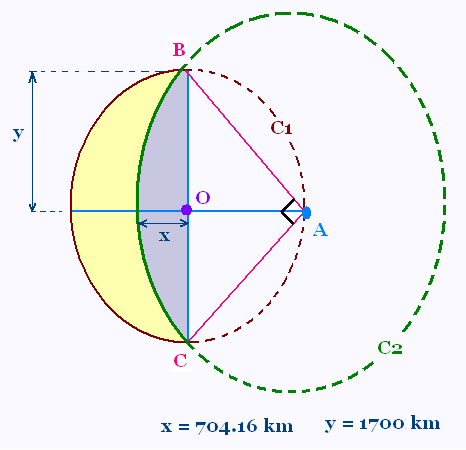
b) L'aire du croissant est égale à la différence entre
la moitié de l'aire du cercle de rayon R1 et celle
de l'aire de la surface plane délimitée par le petit
arc BC de cercle de rayon R2.
Soient:
A1 = moitié de l'aire du cercle de rayon R1 =
πR12/2
A2 = l'aire de la surface plane délimitée par le petit
arc BC de cercle de rayon R2 =
l'aire du secteur BAC - l'aire du triangle ABC.
l'aire du secteur BAC = πR22/4
l'aire du triangle ABC = R12
Donc
A2 = πR22/4 - R12
Ainsi
L'aire du croissant =
πR12/2 - (πR22/4 - R12) =
= πR12/2 - πR22/4 + R12
= R12(π/2 + 1) - πR22/4
= (1700)2(π/2 + 1) - π(2404.16)2/4
= 7429601.38 - 4539589.84 = 2 890 011.54 km2
L'aire du croissant est égale à 2 890 011 km2 .
Soit à peu près 30% de la superficie du
territoire canadien, qui vaut 9 984 670 km2.
Exercice 3: Une coccinelle
Voici une voiture du type "coccinelle" qui roule et qui fait des roulades:
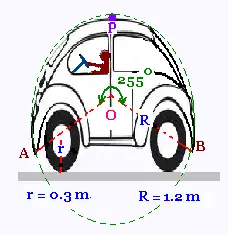
Cette voiture roule sur une certaine distance, ensuite lorsque
le contact au point A touche le sol, la voiture fait une roulade
sur une deuxième distance.
Quel est le nombre minimal de tours que doit effectuer une
roue de l'automobile si la voiture parcourt une distance
de 9 m en effectuant une seule roulade (une seule rotation
du conducteur sur lui même)?
Solution
La voiture s'est déplacé d'une distance d = 9 m
pendant qu'un point (P) sur la voiture effectue une
seule rotation autour du centre O (une seule roulade).
Le long du trajet de cette distance d = 9 m:
- La roulade s'est effectuée sur une distance d1, et
- Les quatre roues ont roulé pendant une distance d2.
Ainsi d = d1 + d2
C1 est la circonférence de la voiture:
C1 = 2πR = 2 x 3.1416 x 1.2 m = 7.54 m
C2 est la circonférence d'une roue:
C2 = 2πr = 2 x 3.1416 x 0.3 m = 1.88 m
La distance d1 est égale à la longueur de l'arc APB.
Calcul de d1:
255°/360° = arc(APB)/C1 = arc(APB)/7.54
Donc d1 = arc(APB) = 7.54 x (255/360) m = 5.34 m
Calcul de d2:
Il reste donc la distance d2 = d - d1 = 9 m - 5.34 m = 3.66 m
qui est la distance au cours de laquelle les quatres roues
ont roulé.
Si une roue (ou quatre) effectue une rotation complète , elle
a roulé C2 = 1.88 m.
Comme elle a roulé 3.66 m, elle doit donc effectuer
3.66/1.88 = 1.94 tours ≈ 2 tours .
La roue (ou quatre) de la coccinelle doit donc effectuer
un minimum de deux tours pour que la voiture se déplace
d'une distance de 9 m.
Exercice 4: Disque de fruits et légumes

Le rayon de ce disque de fruits et légumes est égal
à 3 mètres.
a) Quel est le diamètre du disque?
b) Quelle est la circonférence du disque?
c) Quel est le nombre de secteurs dans le disque?
d) Quel est la mesure de l'angle au centre de chaque secteur?
e) Quel est la mesure des angles des triangles formés par les
secteurs?
f) Quelle est la nature des triangles formés?
g) Quelle est la longueur de l'arc intercepté par
chaque secteur?
h) Quelle est l'aire du disque?
i) Quelle est l'aire de la surface occupée par les
nectarines, si elles représenten 30% du secteur
où elles se trouvent?
j) Quelle est le pourcentage en surface, par rapport au disque
entier, occupée par les nectarines, si elles occupent 30% du secteur
où elles se trouvent?
Exercice 5: Zone entre trois cercles tangents
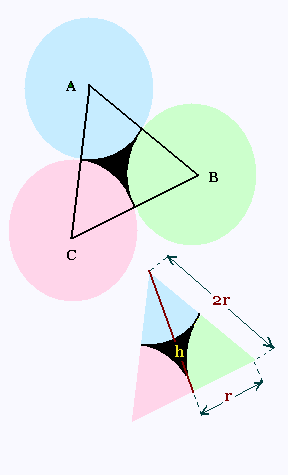
Trois cercles de même rayon sont tangents entre eux.
On s'interesse à la zone délimitée par les trois
petits arcs de cercles interceptés par les angles
au centres A, B et C.
Calculer le périmètre et l'aire de cette zone.
Solution
5.1. Rappels sur un triangle équilatéral
1. Définition du triangle équilatéral
Un triangle équilatéral est un polygone régulier dont
les trois côtés ont même longueur.
1. Propriétés du triangle équilatéral
1. Dans un triangle équilatéral, la médiane,
la hauteur, la bissectrice issues d'un sommet
et la médiatrice du côté opposé sont confondues.
2. Dans un triangle équilatéral, l'orthocentre, le
centre de gravité, le centre du cercle circonscrit et le
centre du cercle inscrit sont confondus.
3. Dans un triangle équilatéral, les angles ont même mesure
qui est égale à 60°.
5.2. Calcul du périmètre
Les trois cercles ont tous le même rayon, donc
AB = BC = CA. Par conséquent, le triangle
ABC est équilatéral. Ainsi les angles A, B et C ont
même mesure, c'est à dire 60°
Le théorème de Pythagore permet d'ecrire:
h2 + r2 = (2r)2
h2 + r2 = 4 r2
h2 = 3 r2
h = r √3
La mesure x du petit arc intercepté par l'angle
au centre A est donnée par la proportion
suivante:
x/2πr = 60°/360° = 1/6
Ainsi x = 2πr/6 = πr/3
La figure géométrique est symétrique, on
aura donc la même mesure pour les deux autres
arc de cercles interceptés par les angles au centres
B et C.
Il vient donc
le périmètre de la zone délimitée par les
trois petits arcs de cercles est égale à
P = 3 x πr/3 = πr
Périmètre = πr
5.3. Calcul de l'aire
L'aire de la zone délimitée par les trois petits
arcs de cercles est égale à la différence entre
l'aire du triangle et celle des trois secteurs.
l'aire du triangle ABC est égale à
(base x hauteur) /2 = (2r x r √3)/2
= r2 √3
L'aire du triangle ABC est égale à r2√3.
l'aire y du secteur d'angle au centre A est
donnée par la formule de la proportion suivante:
60°/360° = 1/6 = y/πr2
y = πr2/6
La figure géométrique est symétrique, on
aura donc la même aire pour les deux autres
secteurs d'angles au centres B et C.
Ainsi l'aire totale des trois secteurs est:
A = 3 x y = 3 x (πr2/6) =
πr2/2
Il vient donc
L'aire de la zone délimitée par les trois petits
arcs de cercles est égale à
r2 √3 - πr2/2 =
r2 (√3 - π/2)
Aire = (√3 - π/2)r2
Application numérique:
r = 1 dm. Donc
Périmètre = πr = 3.1416 x 10 cm = 31.42 cm.
Aire = (√3 - π/2) x (1)2 =
(1.73 - 1.57) = 0.16 dm2 = 16.0 cm2.
Exercice 6: L'arche
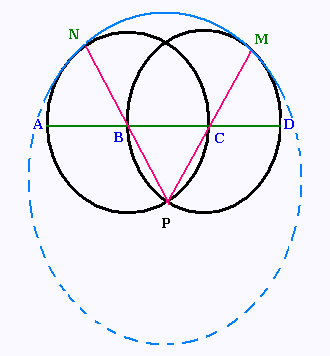
Une arche AD est formée de trois arcs de cercle AN, NM, et MD où
les cercles de centre B et C ont même rayon.
Quelle est la longueur de cette arche?
Solution
Le rayon du cercle de centre B est égal au rayon du
cercle de centre C, donc
AB = BC = CD = BP = BN = CP = CM
AB = BC = CD = BP = BN = CP = CM = r
Par conséquent le triangle BPC est équilatéral.
On a donc: mes(B)= mes(c) = mes (P) = 60°
L'angle au centre C intercepte l'arc MB, donc:
mes(C)/mes(angle plein) = 60°/360° =
(mes de l'arc MD)/2πr
mes de l'arc MD = 2πr x 1/6 = πr/3
Par symetrie, on a
mes de l'arc AN = πr/3
L'arc NM est intercepté par l'angle au centre NPM où
le point P est le centre du cercle de rayoun égal à 2r.
Ainsi
mes(P)/mes(angle plein) = 60°/360° =
(mes de l'arc MN)/2π(2r)
Donc
mes de l'arc MN = 2π(2r) x 1/6 = 2πr/3
mes de l'arc MN = 2πr/3
C'est le double de la mesure précédente de
l'arc MD (= AN).
Ainsi
la mesure de l'arche est égale à
mes de l'arc AN + mes de l'arc NM +
mes de l'arc MD =
πr/3 + 2πr/3 + πr/3 =
4πr/3
La mesure de l'arche est égale à 4πr/3.
Application numérique:
Si AD = 6 m, alors r = 2 m , et donc
La mesure de l'arche = 4 x π x 2 /3 = 8.38 m.
Exercice 7: Tige tournante
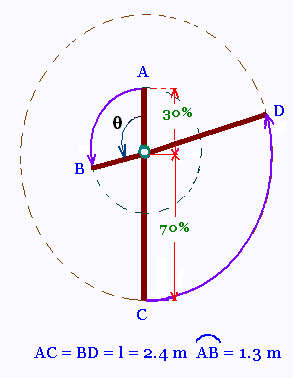
Une tige de longueur AC = BD = l = 2.4 m tourne
d'un arc AB = 1.3 m autour du point O situé à
30% de la longueur l du point A.
Quelle est la longueur de l'arc CD parcouru par l'autre
extrémité de la tige?
Solution
OA = OB = 30% x l = (30/100) x 2.4 = 0.72 m.
OC = OD = 70% x l = (70/100) x 2.4 = 1.68 m.
AB/(2π OA) = θ/360°
θ = 360 x 1.3/(2π x 0.72) = 103.45°
θ = 103.45°
CD/(2π OC) = θ/360° = 103.45°/360°
CD = 2π x OC x 103.45°/360°
= 2π x 1.68 x 103.45/360 = 3.03 m
l'arc CD mesure 3.03 m
Calcul rapide
CD/(2π OC) = θ/360° = AB/(2π OA) . Donc
CD = (2π OC) x AB/(2π OA) = (OC) x AB/(OA) =
AB (OC/OA) = 1.3 x 70/30 = 1.3 x 7/3 = 3.03 m
La donnée de la longueur l = 2.4 m n'est pas pertinente.
|