Mathématiques 2: Géométrie

Quadrilatères
Cerf-volant

1. Définitions

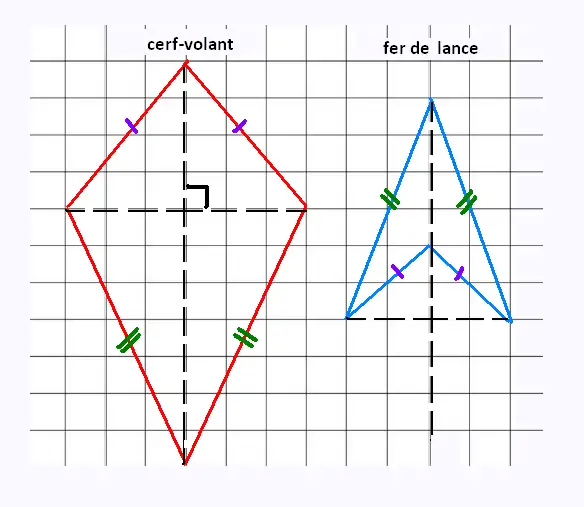
Un cerf-volant est un quadrilatère formé de deux paires de côtés adjacents isométriques.

Un quadrilatère est inscriptible lorsque ses quatre sommets se trouvent tous sur un seul et même cercle. Les sommets sont dits cocycliques. Le cercle est dit circonscrit au quadrilatère.

Dans tout quadrilatère inscriptible (non croisé), les angles opposés sont supplémentaires.

Le carré, le rectangle, et le trapèze isocèle est inscriptible. Un cerf-volant est inscriptible si et seulement s'il a deux angles droits.

Le fait que le cerf-volant ayant deux angles droits est inscriptible montre que l'hypoténuse commune à ses deux angles est nécessairement le diamètre du cercle circonscrit au cerf-volant.

2. Les deux types de cerf-volant

• Si les diagonales se coupent à l'intéreiur du quadrilatère, alors celui est appelé cerf-volant ou cerf-volant convexe.

Si les diagonales se coupent à l'extéreiur du quadrilatère, alors celui est appelé fer de lance ou cerf-volant non convexe.

3. Propriétés du cerf-volant

• Les diagonales d'un cerf-volant sont perpendiculaires.

• La grande diagonale est l'axe de symétrie du cerf-volant.

• L'aire du cerf-volant est égale au demi-produit de ses diagonales.

• Un losange est un cerf-volant dont tous les côtés sont isométriques.

• Un cerf-volant possède un cercle inscrit et un angle ciconscrit.

4. Cercle inscrit dans un cerf-volant

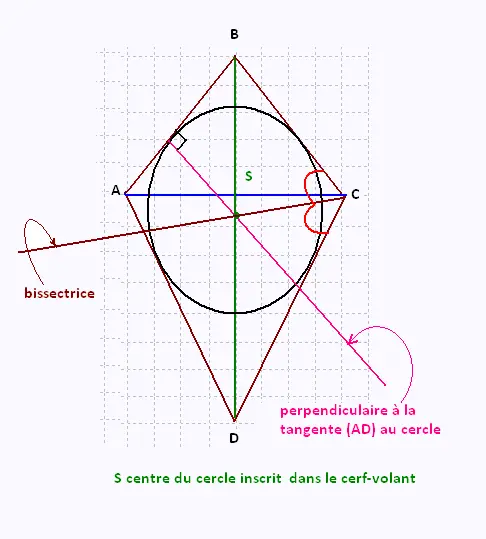
Un cerf volant possède un cercle inscrit.

Le centre du cercle inscrit dans un triangle est le point d'intersection des bissectrices des angles de ce triangle.

Par conséquent,

• Le centre de ce cercle est le point d'intersection de la grande diagonale et de la bissectrice de l'angle qui lui est opposée.

• Le centre de ce cercle c'est aussi le point d'intersection de la grande diagonale et de la médiatrice de l'un des côtés du cerf-volant.

5. Cercle circonscrit au cerf-volant

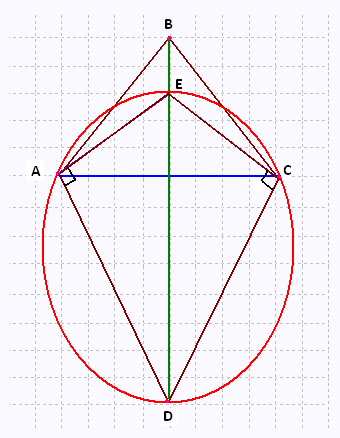
Un cerf-volant est inscriptible si et seulement s'il a deux angles droits.

Le fait que le cerf-volant ayant deux angles droits est inscriptible montre que l'hypoténuse commune à ses deux angles est nécessairement le diamètre du cercle circonscrit au cerf-volant.

Le cerf-volant ABCD n'est pas inscriptible dans un cercle.

Le cer-volant AECD est inscriptible dans le cercle parce qu'il possède deux angles droits.

6. Exercice 1

Énoncé:



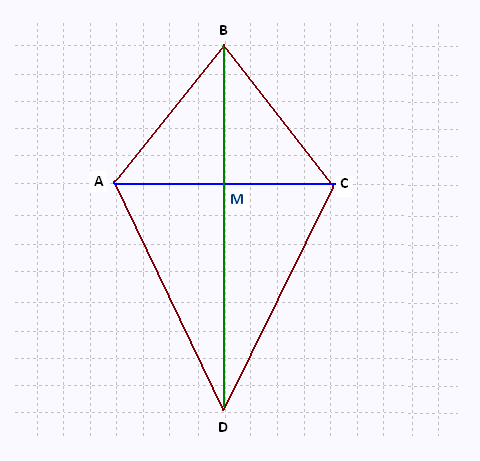
Le quadrilatère ABCD est un cerf-volant.

a) Démontrer que les diagonales de ce quadrilatère sont perpendiculaires.

b) Démontrer que les angles obtus sont isométriques.

c) Déterminer la position du cercle inscrit à ce quadrilatère.

d) Déterminer la position du cercle circonscrit à ce quadrilatère.

Réponse:

• Le quadrilatère ABCD est un cerf-volant.

Puisque le qudrilatère ABCD est un cerf-volant, les triabgles ABC et ADC sont isocèles.

La hauteur issue du point B qui coupe [B,C] en M est à la fois bissectrice de l'angle B, médiane et médiatrice du segment [B,C]. D'où:

AM = MC

Pour le triangle isocèle ADC, AM = MC signifie que le point M est milieu de [A,C], donc le segment [D,M] est la médiane de la base [B,C] de ce triangle.

Cette médiane [D, M ] est donc médiatrice de [A,C], bissectrice de l'angle D et hauteur issue du sommet D.

Le point M est commun à ces deux triangles isocèles. Si [D,M] et [B,M] sont simultanément les médiatrices du segment [A,C], alors la droite (DB) est la médiatrice du segment [A,C]. Celà signifie que les diagonales [A,C] et [D,B] du cerf-volant sont perpendiculaires.

Énoncé:



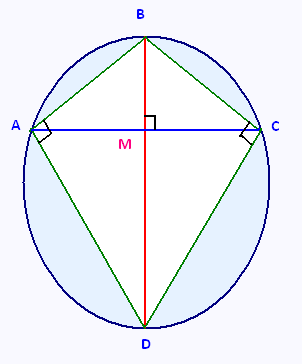
On considère un cerf-volant ABCD inscrit dans un cercle de rayon égal à 6 cm. La diagonale BD du cerf-volant est un diamètre du cercle.

Le point d'intersection M des diagonales BD et AC du quadrilatère se situe, à partir de du point B, au tiers du diamètre BD du cercle circonscrit au cerf-volant.

On demande l'aire de la surface entre le cercle et le cerf-volant.

Réponse:

• On sait que :

. le diamètre BD du cercle circonscrit au quadrilatère est une des diagonales du cerf-volant, et mesure 12 cm,
. Le quadrilatère ABCD est un cerf-volant,
. L'intersection des diagonales du quadrilatère est au tiers du diamètre à barir du point B.

. Calcul de BM:

BM = (1/3) BD = (1/3) 12 = 4 cm. D'où DM = 12 - 4 = 8 cm

BM = 4 cm
DM = 8 cm

. Calcul de CM:

. Le triangle DBC est rectangle d'après la propriété « Si un triangle est inscrit dans un cercle de diamètre l'un des côtés du triangle, alors ce triangle est rectangle ».

. La relation métrique dans ce triangle rectangle s'ecrit:

CM² = BM x MD. Donc:

CM² = 4 x 8 = 32. D'où:

CM = 4√2 cm.

. Calcul de l'aire A1 du triangle DBM:

A1 = CM x BD/2 = 4√2 x 12 /2 = 24√2

A1 = 24√2 cm ²

Par symétrie, l'aire du triangle DBA est égale à celle de A1.

Ainsi l'aire du cerf-volant = 2 x 24√2 = 48 √2 cm².

L'aire du cerf-volant = 48 √2 cm².

. Calcul de l'aire du cercle:

Aire du cercle = π (BD/2)² = π (12/2)² = 36 π

L'aire du cercle = 36 π cm².

. Calcul de l'aire entre le cercle et le cerf-volant:

L'aire entre le cercle et le cerf-volant = l'aire du cercle moins l'aire du cerf-volant = 36 π - 48 √2 cm².

L'aire entre le cercle et le cerf-volant =
36 π - 48 √2 cm² = 45.2 cm².

• L'aire entre le cercle et le cerf-volant mesure environ 45 cm².