Mathématiques 23: Géomrtrie
Théorème de Ceva
1. Théorème de Ceva
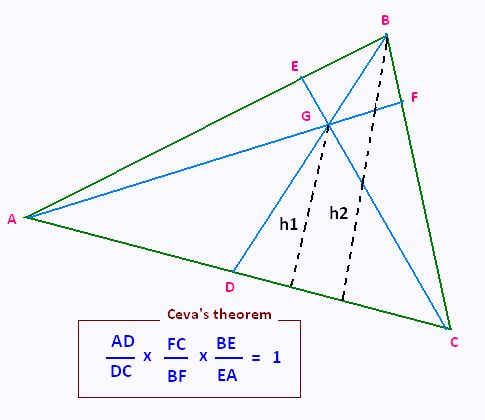
AD/DC = (AD h1 /2)/(DC h1 /2) = ADG/GDC
AD/DC = (AD h2 /2)/(DC h2 /2) = ADB/BDC
Donc:
AD/DC = ADG/GDC = ADB/BDC =
(ADB - ADG)/(BDC - GDC) = ABG/BGC
De même:
BF/FC = ABG/AGC, et
BE/EA = GBC/AGC
D'où:
AD/DC x FC/BF x BE/EA =
ABG/BGC x AGC/ABG x GBC/AGC = 1
AD/DC x FC/BF x BE/EA = 1
AD/DC x FC/BF x BE/EA = 1
2. À propos de Giovanni Ceva

Giovanni Ceva (Milan, 1647 – Mantoue juin 1734) était un mathématicien italien. Il est réputé pour l'important théorème de géométrie du triangle qu'il a redécouvert et qui porte son nom : le théorème de Ceva.
Le théorème de Ceva donne une condition nécessaire et suffisante pour que trois droites passant par les trois sommets d'un triangle soient concourantes.
3. Relation des proportions
Si a/b = c/d, alors:
a/b = c/d = k → a = b k et c = d k
Donc
(a + c)/(b + d) = k(b + d)/(b + d) = k , et
(a - c)/(b - d) = k(b - d)/(b - d) = k
On a toujours:
a/b = c/d = (a + c)/(b + d) = (a - c)/(b - d)
|