Maths
- 2 -
Géométrie
© The scientific sentence. 2010
| |
| Mathématiques: Géométrie
Démonstration d'un résultat en Géométrie
1. Introduction
Une démonstration mathématique est un raisonnement logique qui s'appuie sur des résultats théoriques déjà établis pour pavenir à la conclusion cherchée.
Exemple:
On veut savoir la mesure du troisième angle d'un triangle.
ABC est un triangle quelconque.
On donne
mes(∠ A) = 70° et mes(∠B) = 60°.
Quelle est la mesure de l'angle C?
On fait appel à la propriété la plus adaptée au problème qui est celle de la somme des mesures des angles intérieurs d'un triangle
suivante:
La somme des mesures des angles intérieurs
d'un triangle est égale à 180°.
D'après cette propriété, on ecrit:
70° + 60° + mes(∠ C) = 180°.
D'où:
mes(&angle C) = 180° - 70° - 60° = 50°. ;
mes(∠ C) = 50°.
2. La méthode

Pour démontrer un résultat, on doit:
• Identifier les données utiles de l'énoncé,
• Utiliser les résultats théoriques déjà établis (théorèmes, propriétées, formules), et
• Déduire la conclusion.
3. La démonstration en Mathématiques
On note bien qu'une démonstration en Mathématiques
s'appuie sur des définitions, des propriétés, des théorèmes, ou des formules clairement prouvés à l'avance.
Le but d'une démonstration en Mathématiques est de prouver
la validité ou la non validité d'un énoncé, c'est à dire soit il est vrai, soit il est faux.
Une constatation ou une mesure sur un dessin ne justifient pas
la validité d'un énoncé en géométrie.
La multiplicité des exemples qui vérifient un énoncé ne suffisent pas à
prouver qu'il est vrai.
Mais un contre-exemple suffit pour invalider un énoncé.
4. La démonstration en Géométrie
Démontrer un résultat en Géométrie se fait
généralement en plusieurs étapes. Toutes ces étapes
ont la même structure composée de:
• Par hypothèse,
• Or
• Donc
Il est très important de rédiger une démonstration avec de la rigeur et de la clarté.
Il est aussi important d'utiliser des termes précis.
Ce sont:
On sait que ...,
Par hypothèse ...
Si ..., alors...,
Par conséquent...,
D'après le théorème ... ,
D'après la réciproque du théorème ... ,
C'est à dire ...,
En utlisant ...
or ...,
En vertu de ...
Conformément à ...
Selon ...,
Si et seulement si ... ,
Il vient ... ,
Ainsi ... ,
Donc ... ,
On en déduit que ... ,
On obtient ... ,
...
5. Exemples
Exemple 1: Réciproque du théorème de Thalès
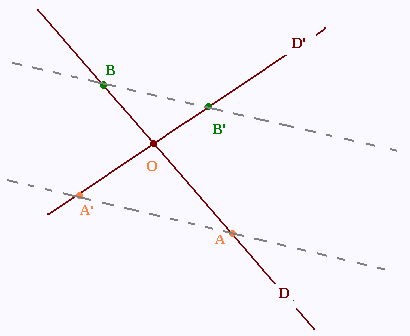
Soient (D) et (D') deux droites sécantes en O.
Soient A et B deux points de (D) distincts de O.
Soient A' et B' deux points de (D’) distincts de O.
On a OA/OB = OA'/OB'.
De plus,
les points O, A, B et les points O, A', B'sont alignés dans le même ordre.
D'après la réciproque du théorème de Thalès on déduit que les droites (AA') et (BB') sont parallèles.
Exemple 2: Théorème de Pythagore
ABC est un triangle rectangle en A.
On donne AB = 4 cm, et AC = 3 cm.
Quelle est la mesure de côté BC?
On sait que ABC est un triangle rectangle en A.
D'après le théorème de Pythagore, on ecrit:
BC2 = AC2 + AB2 =
32 + 42 = 25.
D'où:
BC = √25 = 5.
BC = 5 cm.
Exemple 3: Cercle circonscrit au triangle rectangle
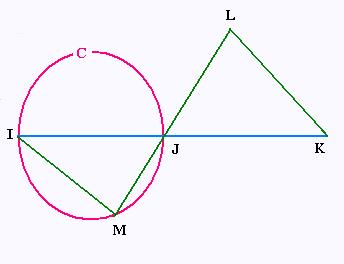
JKL est un triangle tel que : JK = 6 cm ; JL = 3,6 cm et KL = 4,8 cm.
J est un point du segment [IK] et IJ = 9 cm.
C est le cercle de diamètre [IJ].
La droite (JL) coupe le cercle C en M.
1. Démontrer que le triangle JKL est rectangle.
2. Justifier que le triangle IJM est rectangle.
3. Déterminer la longueur JM.
1.
62 = (3.6)2 + (4.8)2
D'après la réciproque du théorème de Pythagore, le triangle
JKL est rectangle en L.
2.
[IJ] est le diamètre du cercle.
D'après la propriété:
Si un triangle est défini par le diamètre d’un cercle et un autre
point du cercle, alors ce triangle est rectangle,
le triangle IJM est rectangle en M.
3.
Les angles ∠M et ∠L sont égaux. Ils sont alternes internes
au droites (LK) et (IM). Ainsi ces droites
(LK) et (IM) sont parallèles.
Les droites (LK) et (IM) sont parallèles.
les droites (ML) et (IK) sont sécantes en J.
Alors le théorème de Thalès s'ecrit:
JL/JM = JK/JI = KL/IM
D'où:
JM = JL x JI/JK = 3.6 x 9/6 = 5.4 cm
JM = 5.4 cm.
|
|