Maths
- 2 -
Géométrie
© The scientific sentence. 2010
| |
| Mathématiques 45: Géométrie:
Distance entre deux points
dans un plan cartésien
1. Définition
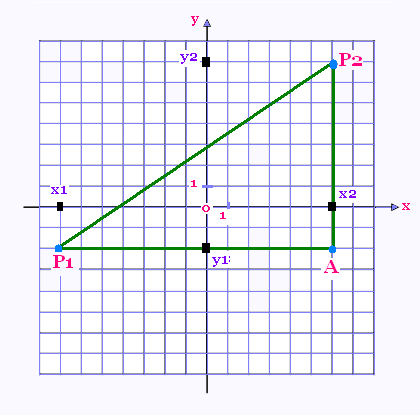
La distance entre deux points P1 et P2, notée
d(P1, P2), dans le plan cartésien, est
le plus petit trajet entre ces deux points.
Le calcul de cette distance s'appuit sur la
relation de Pythagore.
Dans la figure, On trace le segment P1P2. Ensuite
on forme un triangle AP1P2 rectangle en A.
P1P2 est l'hypoténuse, AP1 et AP2 sont les cathètes
du triangle rectangle AP1P2.
La formule de Pythagore s'ecrit:
P1P22 = AP12 + AP22.
L'abscisse du point A = l'abscisse du point P2 = x2
L'ordonnée du point A = l'ordonnée du point P1 = y1
La mesure du segment P1P2 est égale à la distance d(P1, P2).
La mesure du segment P1A est égale à la différence
entre l'abscisse du point P2 et celle du point P1;
soit Δx = x2 - x1.
La mesure du segment AP2 est égale à la différence
entre l'ordonnée du point P2 et celle du point P1 ;
soit Δy = y2 - y1.
Ainsi
(d(P1, P2))2 = (x2 - x1)2 + (y2 - y1)2
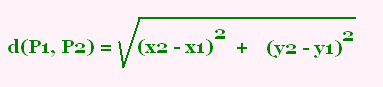
On note:
. La distance entre P1 et P2 est positive ou nulle.
. La distance entre P1 et P2 est égale à la distance entre P2 et P1:
d(P1, P2) = d(P2, P1)
2. Exemples
2.1. Exemple 1
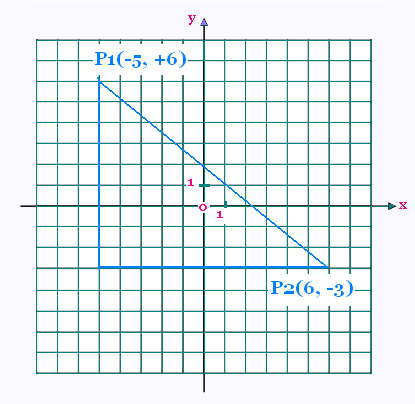
La distance entre P1 et P2 est:
d(P1,P2) = √[(6 + 5)2 + (6 + 3)2] =
√[112 + 92] = √202 = 14.21 unités.
2.2. Exemple 2
Quelle est la distance entre deux points de
coordonnées ( + 5, - 1) et (- 3, 0) ?
Cette distance est égale à :
√[(- 3 - 5)2 + (0 + 1)2] =
√[82 + 12] = √65 = 8.1 unités.
2.3. Exemple 3
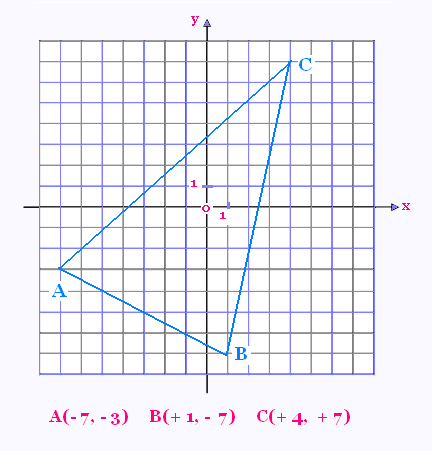
a) Quel est le périmètre du triangle ABC ?
Dans ce repère 1 carreau = 1 dm x 1 dm.
d(A, B) = √[(1 + 7)2 + (- 7 + 3)2] =
√[82 + 42] = 8.94 dm.
d(B, C) = √[(4 - 1)2 + (7 + 7)2] =
√[32 + 142] = 14.32 dm.
d(A, C) = √[(4 + 7)2 + (7 + 3)2] =
√[112 + 102] = 14.86 dm.
Le périmètre du traingle ABC =
d(A,B) + d(B,C) + d(C,A) =
8.94 + 14.32 + 14.86 = 38.12 dm.
|
|