Maths
- 2 -
Géométrie
© The scientific sentence. 2010
| |
| Mathématiques 45: Géométrie:
Distance d'un point à une droite
1. Distance d'un point à une droite
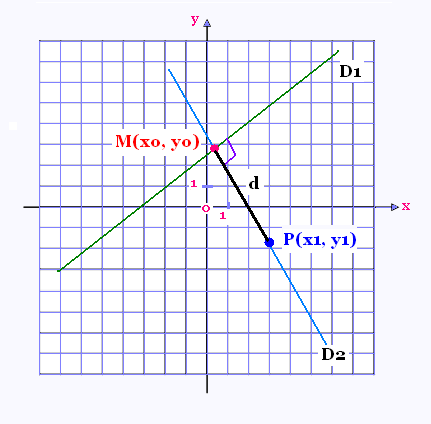
On veut calculer la distance d'un point quelconque
P(x1, y1) à une droite D1 déquation:
D1: Ax + By + C = 0 (1),
Soit
D2: y = a2 x + b2 (2)
l'équation de la droite sur laquelle se trouve
le point P et qui est perpendiculaire à D1.
Les droites D1 et De se rencontrent au point M(xo,yo).
Ecrivons l'équation de la droite D1 sous forme
fonctionnelle:
D1: y = a1 x + b1 (1'),
avec a1 = - A/B et b1 = - C/B
M(xo, yo) ∈D1 → yo = a1 xo + b1 (3),
M(xo, yo) ∈D2 → yo = a2 xo + b2 (4),
Comparons (3) et (4):
a1 xo + b1 = a2 xo + b2 . On obtient:
xo = (b1 - b2)/(a2 - a1) (5),
P(x1, y1) ∈D2 → y1 = a2 x1 + b2 (6),
d'où b2 = y1 - a2 x1
Substituons cette valeur de b2 dans (5), on obtient:
xo = (b1 - y1 + a2 x1)/(a2 - a1) (5'),
Sustrayons (4) de (6), on obtient:
y1 - yo = a2(x1 - xo) (7),
D1 est perpendiculaire à D2. Donc a1 a2 = - 1
ou a2 = - 1/a1 (8),
La distance d = d(P, M) a pour expression:
d2 = (x1 - xo)2 + (y1 - yo)2
Utilisons (7), on obtient:
d2 = (x1 - xo)2 + a22(x1 - xo)2 =
(x1 - xo)2(1 + a22)
Avec (5'), on obtient:
d2 = [x1 - ((b1 - y1 + a2 x1)/(a2 - a1))]2(1 + a22)
= [x1(a2 - a1) - (b1 - y1 + a2 x1)]2(1 + a22)/(a2 - a1)2
= [x1a2 - x1a1 -b1 + y1 - a2 x1]2(1 + a22)/(a2 - a1)2
= [- x1a1 - b1 + y1]2(1 + a22)/(a2 - a1)2
Utilisons (8):
1 + a22 = 1 + 1/a12 = (1 + a12)/a12
(a2 - a1)2 = (- 1/a1 - a1)2 = (1/a1 + a1)2 =
(1 + a12)2 /a12
Donc:
(1 + a22)/(a2 - a1)2 = 1/(1 + a12)
avec a1 = - A/B et b1 = - C/B , on a:
d2 = [(A/B)x1 + (C/B) + y1]2B2/(A2 + B2)
= [Ax1 + C + By1]2 /(A2 + B2)
= [Ax1 + By1 + C]2 /(A2 + B2)
Ainsi:
d = |Ax1 + By1 + C|/√(A2 + B2)
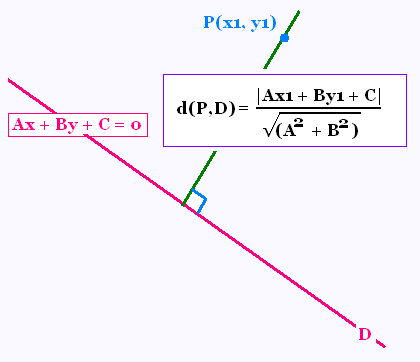
d est la distance d'un point
(x1, y1) à une droite
d'équation Ax + By + C = 0.
2. Exemples
2.1. Exemple 1
Quelle est la distance du point (- 3, + 4) à la droite
d'équation:
y = - (3/2) x + 5
Ecrivons d'abord cette équation sous sa forme
générale:
y +(3/2) x - 5 = 0 ou 3x + 2y - 10 = 0
d = |(3)(- 3) + (2)(+ 4) - 10|/√(32 + 22) =
|- 9 + 8 - 10|/√(9 + 4) =
11/√13 = 11 √13/13.
d = 11√13/13.
2.2. Exemple 2
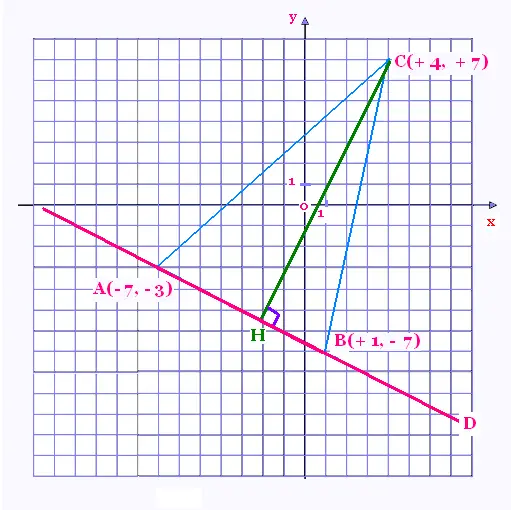
Quelle est l'aire du triangle ABC ?
Dans ce repère 1 carreau = 1 dm x 1 dm.
On considère la droite D passant par les deux points
A(- 7, - 3) et B(+ 1, - 7).
On dresse la perpendiculaire du sommet C qui coupe AB
en H. Le segment CH est la distance du
point C à la droite D.
L'aire du triangle ABC = CH x AB/2
Sous sa forme fonctionnelle, l'équation de la droite
D s'ecrit:
D: y = a x + b (1)
Donc:
Point A ∈ D: - 3 = - 7a + b (2)
Point B ∈ D: - 7 = a + b (3)
Soustrayons (3) de (2), on trouve:
4 = - 8 a → a = - 1/2
d'où b = - 7 - a = - 7 + 1/2 = - 13/2
l'équation (1) devient:
y = - (1/2) x - 13/2
Sous forme gérérale:
2y = - x - 13 ou
D: x + 2y + 13 = 0
1. On calcule la distance d(C, H):
d(C, H) = |(1)(+ 4) + (2)(+ 7) + 13|/√(12 + 22) =
d(C, H) = 31/√5 = 31√5/5
d(C, H) = 31√5/5.
2. On calcule la distance d(A, B):
d(A, B) = √[(1 + 7)2 + (- 7 + 3)2] =
√[64 + 16] = √80 = 4 √5
d(A, B) = 4 √5 .
Il vient:
L'aire du triangle ABC = d(C, H) x d(A, B)/2 =
31 √5/5 x 4 √5 /2 =
31 √ x √5 x 5/5 x 4 /2 =
31 x 5 x 5/5 x 2 = 31 x 5 x 2 = 310 dm2.
L'aire du triangle ABC = 310 dm2.
|
|