Mathématiques 45: Géométrie:
Droites parallèles, droites perpendiculaires et
droites sécantes
1. Droites parallèles
1.1. Règle
Deux droites sont parallèles si elles ont une
même pente.
D1: y = a1 x + b1
D2: y = a2 x + b2
On a: a1 = a2.
Si b1 ≠ b2, les droites sont disjoints.
Si a1 ≠ 0 et a2 ≠ 0, les droites sont obliques.
Si a1 = a2 et b1 = b2, les droites sont parallèles confondues.
1.2. Exemples
1.
Les droites d'équations respectives:
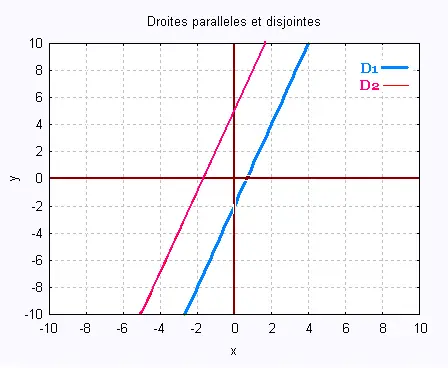
y = 2 x + 3, et
y = 2 x - 7
sont parallèles.
Les ordonnées à l'origine sont différentes :
+ 3 ≠ - 7. Elles sont donc disjointes.
2.
Trouver l'équation de la droite D1, parallèle disjointe
à la droite D2 d'équation: y = 3 x + 5, et qui doit passer
par le point P(2, 4)?
D1 : y = a1 x + b1
D2 : y = 3 x + 5
D1 ∥ D2 → a1 = 3.
D1 passe par le point (2, 4) → 4 = (3)(2) + b1
C'est à dire: 4 = 6 + b1
d'où b1 = - 2
Ainsi l'équation de la droite cherchée est :
D1: y = 3 x - 2
2. Droites sécantes
2.1. Règle
Deux droites sont sécantes si elles n'ont pas
la même pente.
D1: y = a1 x + b1
D2: y = a2 x + b2
On a: a1 ≠ a2.
2.2. Exemples
1.
Les droites d'équations respectives:
y = 2 x + 3, et
y = - 4 x - 7
sont sécantes.
Les ordonnées à l'origine peuvent être égales
ou différentes
.
2.
Trouver une droite sécante à la droite d'équation
y = - 6 x + 12 ?
Il suffit d'une équation avec une pente différente
de - 6. Par exemple : y = 4 x + 1.
3. Droites perpendiculaires
2.1. Règle
Deux droites sont perpendiculaires si la pente de
l'une est égale à l'opposé de l'inverse de l'autre.
Autrement dit, le produit des pentes est égale à - 1.
D1: y = a1 x + b1
D2: y = a2 x + b2
On a: a1 = - 1/a2, ou
a1 . a2 = - 1
2.2. Exemples
1.
Les droites d'équations respectives:
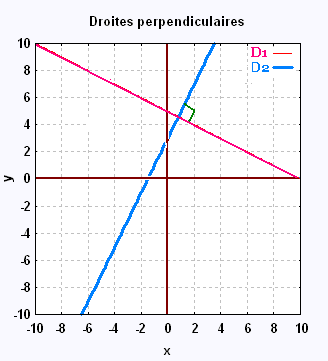
y = 2 x + 3, et
y = - 0.5 x - 7
sont perpendiculaires.
Les ordonnées à l'origine peuvent être égales
ou différentes
.
Les droites perpendiculaires sont toujours sécantes.
2.
Trouver l'équation d'une droite perpendiculaire à la
droite d'équation y = - 6 x + 12 ?
Il suffit d'une équation avec une pente égale à
l'opposé de l'inverse de - 6. C'est à dire +1/6.
Par exemple y = (1/6) x - 4.
3.
Trouver l'équation d'une droite D1 perpendiculaire à la
droite D2 d'équation y = - (1/2) x + 5 et passant par le
point P(0, 3).
D1: y = a x + b, l'équation cherchée.
D1 ⊥ D2 → a = + 2
.
D1 passe par P → 3 = (2)(0) + b
D'où b = 3.
Ainsi l'équation de la droite D1 est:
y = 2 x + 3
|