Mathématiques 2: Géométrie
Droites et plans dans l'espace

1. La droite

Une droite est un espace à une dimension. C'est comme un fil d'épaisseur nulle qui s'étend à l'infini et qui n'a pas de bornes.

Un couple de points (A, B) définit la droite (AB).

Une droite est définie par deux points distincts.

La droite contenant les points A et B se nomme la droite (AB).

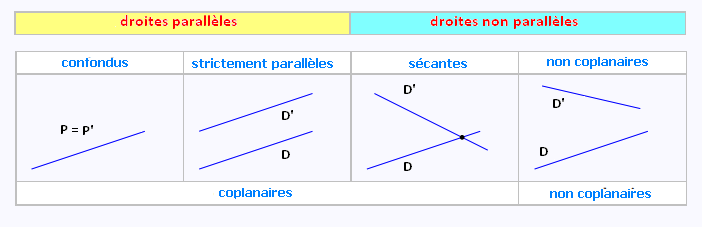
Deux droites sont parallèles si et seulement si elles sont confondues ou si elles n'ont aucun point commun.

Deux droites ayant un et un seul point commun sont dites sécantes.

Si deux droites sont parallèles à une même troisième droite, alors elles sont parallèles entre elles.

• Par un point A n'appartenant pas à une droite D, on ne peut faire passer qu'une droite parallèle à D.

Positions relatives de deux droites



• Soit deux droites parallèles D et D', toute droite sécante à D est sécante à D'.
• Soit deux droites parallèles D et D', toute droite perpendiculaire à D est perpendiculaire à D'.
• Soit deux droites parallèles D et D', toute droite parallèle à D est parallèle à D'.

Deux droites sont dites perpendiculaires lorsqu'elles se coupent en formant un angle droit. Les directions des droites étant orthogonales. les droites sont dites aussi orthogonales.

• Si deux droites sont perpendiculaires, toute droite parallèle à l'une est perpendiculaire à l'autre.
• Si deux droites sont parallèles, toute droite perpendiculaire à l'une est perpendiculaire à l'autre.
• Si deux droites sont perpendiculaires à une même droite alors elles sont parallèles entre elles.

Deux droites incluses dans un même plan sont dites coplanaires.

Deux droites de l’espace sont soit coplanaires soit non coplanaires :

2. Le plan

Un plan est un espace à deux dimensions. C'est comme une feuille d'épaisseur nulle qui s'étend à l'infini et qui n'a pas de bords.

Un triplet de points (A, B, C) non-colinéaires définit le plan (ABC).

L'espace contenant les points A, B, et C se nomme le plan (ABC).

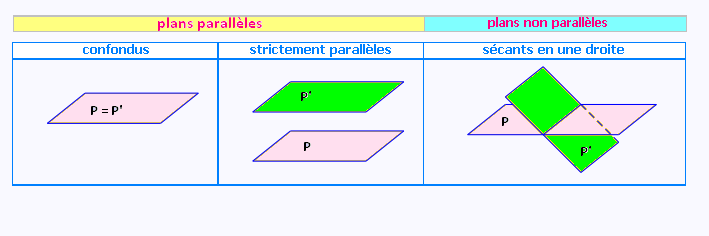
Positions relatives de deux plans

Deux plans sont soit sont confondus , soit strictement parallèles , soit sécants .

L'intersection de deux plans est une droite, appelée droite d’intersection.

Deux plans sont parallèles lorsqu’ils sont confondus ou lorsqu’ils n’ont aucun point commun.

Deux plans sont parallèles si et seulement si deux droites sécantes d’un des deux plans sont parallèles à deux droites de l’autre plan.



Un plan coupe deux plans parallèles suivant deux droites parallèles.

Deux plans sont parallèles si et seulement si deux droites sécantes de l’un sont respectivement parallèles à deux droites sécantes de l’autre.

Deux plans confondus sont considérés comme parallèles.

3. Droites et plans

Deux droites sont dites coplanaires lorsqu’elles sont contenues dans un même plan.

Deux droites sont dites non-coplanaires lorsqu’elles ne sont pas contenues dans un même plan.

Deux droites sont dites strictement parallèles lorsqu’elles sont coplanaires et parallèles.

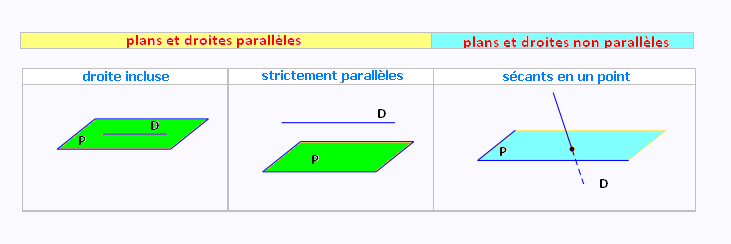
Positions relatives d’une droite et d’un plan

Une droite est soit incluse dans un plan, soit strictement parallèle à un plan, soit t sécante à un plan.

4. Exercices

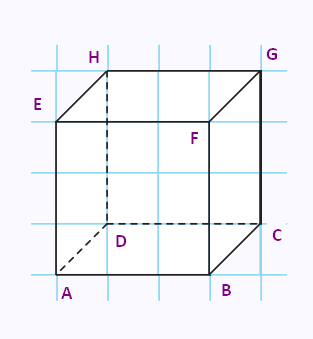
1. Cube et droites

On considère un cube ABCDEFGH.
1) Représenter ce cube en perspective cavalière.

2) a) Justifier que EFCD est un parallélogramme.
b) En déduire que la droite (FC) est parallèle au plan (EBD).

3) a) Montrer que la droite (FH) est parallèle au plan (EBD).
b) En déduire la position relative des plans (FCH) et (EBD).

Réponse



2) a) Le solide ABCDEFFGH est un cube. Ses douzes arêtes sont donc parallèles quatre à quatre. D'où: (EF)//(DC)



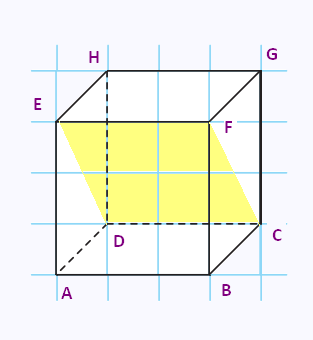
De plus, les plans opposés (ADHE) et (BCGF) sont parallèles. Donc les droites incluses (ED) et (FC) sont parallèles: (ED)//(CF)

Le quadrilatère EFCD a des côtés opposés parallèles deux à deux, c'est donc un parallélogramme.

b)



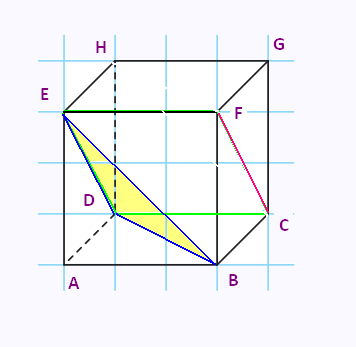
La droite (ED) est incluse dans le plan (EBD). Les droites (ED) et (CF) sont parallèles, donc la droite (FC) est parallèle au plan (EBD).

3) a) Les faces planes EHGF et ADCB du cube sont parallèles. Donc les droites formées par les diagonales [FH] et [BD] sont parallèles: (FH) //(DB).

De plus, la droite (DB) est incluse dans le plan (EDB). La droite (FH) est donc parallèle au plan ((EDB).

b)



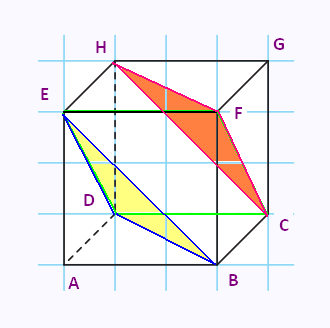
La droite (FH) est incluse dans le plan (FCH), la droite (DB) est incluse dans le plan (EBD), FH) //(DB), donc les plans (FCH) et (EDB) sont parallèles.

Ses deux plans ne sont pas confondus, ce sont donc des plans strictement parallèles.

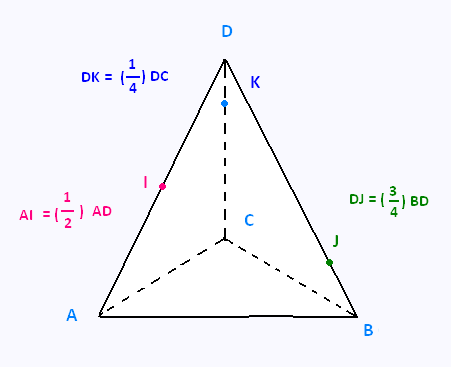
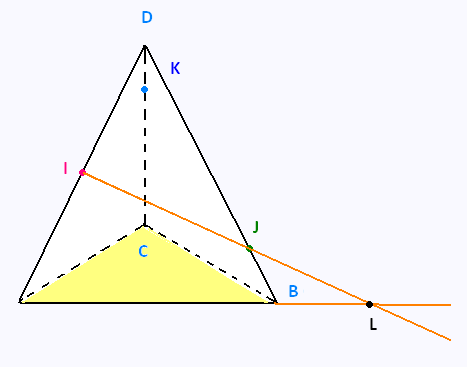
2. Tétraèdre

ABCD est un tétraèdre. I est lemilieu de [AD], J ? [BD] et K ? [CD] tels que DJ = 0, 75BD et DK = 0, 25DC.

1) Représenter ce tétraèdre en perspective cavalière et y placer les points I, J, K.

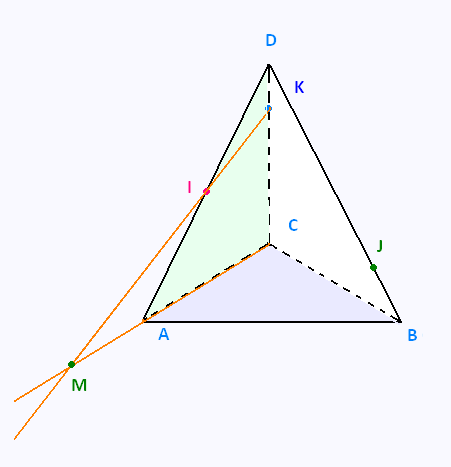
2) Déterminer et construire (s’ils existent) les points :

a) L, intersection de la droite (I J) et du plan (ABC) ;
b) M, intersection de la droite (IK) et du plan (ABC).

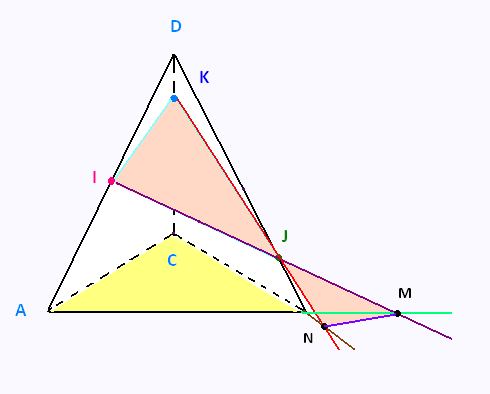
3) Déterminer, en justifiant, l’intersection du plan (I JK) et du plan (ABC).

Réponse

1)


2) a)


b)


3)


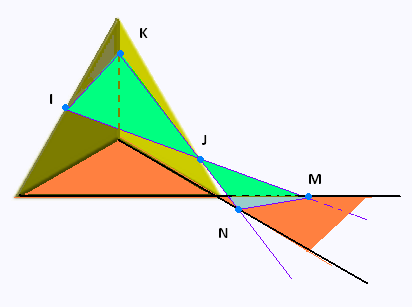
Un peu plus clairement,

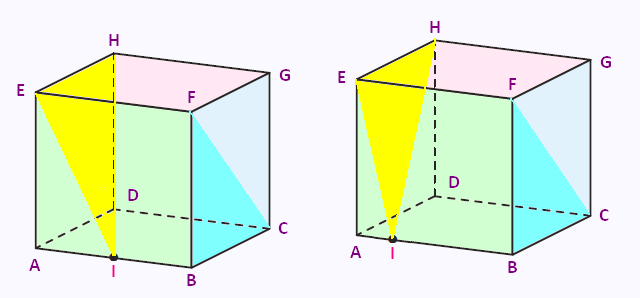
4. Plans des cubes

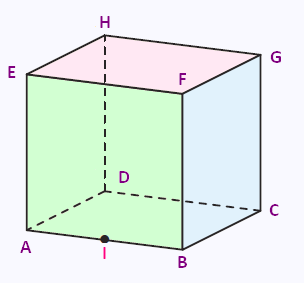
1) Reproduire la figure ci-dessus et y replacer le point I.

2) Construire sur cette figure :

• les intersections des plans (EHI) et (AFB)
• les intersections des plans (EHI) et (HDG)
• les intersections des plans (EHI) et (BDF)
• les intersections des plans (EHI) et (FBC).


Réponse

les intersections des plans (EHI) et (AFB)


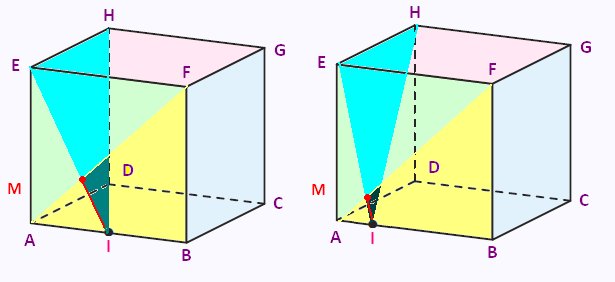
• Segment [MI].



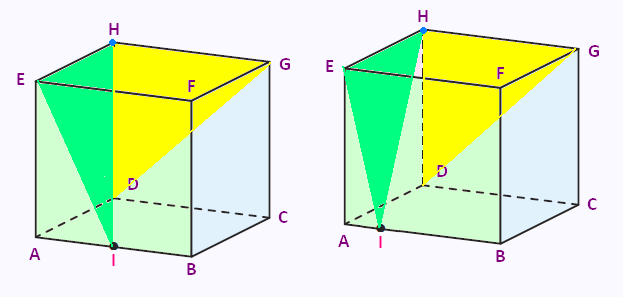
• Point H.



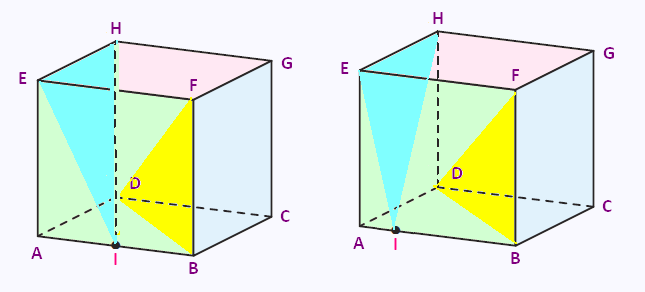
• Aucun point d'intersection.



• Aucun point d'intersection.