Mathématiques 34:Géométrie
Conjecture et preuve
Carré et triangle équilatéral

Points alignés dans un pentagone irrégulier

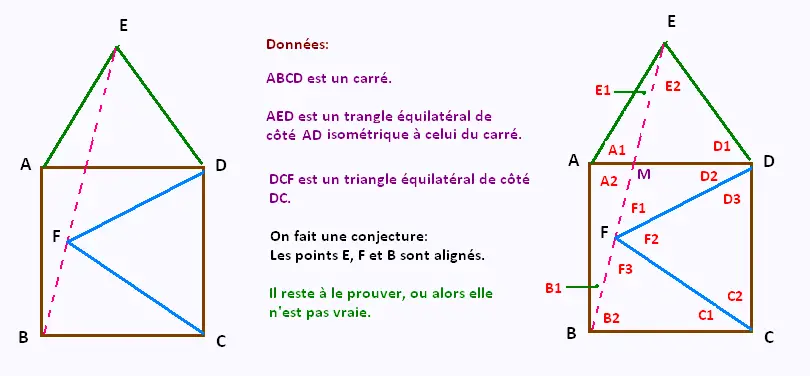
Hypothèses:

Trois points E, F et B sont alignés si l'angle EFB, qu'ils formnet, est un angle plat.

Nous allons démontrer cette propriété pour les points E, F et B en utilsant la propriété des angles intérieurs d'un triangle:

La somme des mesures des angles intérieurs d'un triangle est égale à 180^o.

• D'après la propriété "les angles d'un triangle équilatéral mesurent chacun 60^o", on a:

D1 = A1 = D3 = F2 = C2 = 60^o.

mes(F2) = 60^o.

• Donc les mesures de leurs complémentaires sont:

C1 = D2 = 30^o.

Puisque CF = CB, le triangle BFC est isocèle, donc les angles à la base sont isométriques. d'où:

B2 + F3 + C1 = 2 F3 + 30 = 180 . Il vient donc:

F3 = B2 = (180 - 30)/2 = 75^o.

mes(F3) = 75^o.

• Le complémentaire de B2 mesure alors 90 - 75 = 15^o.

ABCD est un carré, donc les droites (BC) et (AD) sont parallèles. D'où B2 et M sont supplémentaires.

M = 180 - B2 = 180 - 75 = 105^o.

Dans le triangle MF1D2, F1 = 180 - M - D2 = 180 - 105 - 30 = 45^o.

mes(F1) = 45^o.

• On fait la somme des trois angles F1, F2, et F3.

mes(F2) + mes(F3) + mes(F1) = 60 + 75 + 45 = 180^o.

mes(F2) + mes(F3) + mes(F1) = 180^o.

Conclusion:

Les point E, F et B sont alignés. La conjecture est vraie.