Mathématiques 2: Géométrie:
Exercices divers:
Triangles et parallélogrammes
Exemple 1
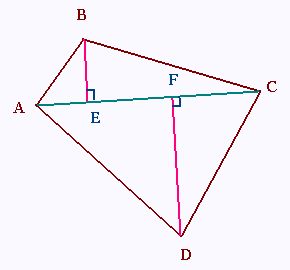
ABCD est un quadrilatère tel que AC = 4 cm,
BE = 1 cm et FD = 1.5 cm.
a)
a.1) L'aire du triangle ABC = (AC x BE)/2 =
(4 x 1)/2 = 2 cm2
a.2) L'aire du triangle ADC = (AC x DF)/2 =
(4 x 1.5)/2 = 3 cm2
b) L'aire du quadrilatère ABCD =
l'aire du triangle ABC + l'aire du triangle ADC =
2 + 3 = 5 cm2
Exemple 2
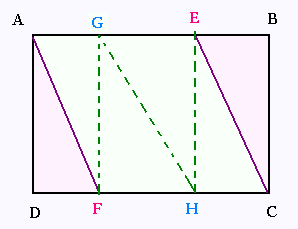
On veut calculer l'aire du parallélogramme AECF obtenu en traçant des segments de droites parallèles à partir des sommets A et C.
On découpe le parallélogramme AECF à
l'intérieur du rectangle ABCD en quatre
triangles AGF, FGH, HGE, et HEC.
Avec AB = 10 cm, AD = 6 cm et AE = 6.4 cm.
L'aire du parallélogramme AFCE =
L'aire de ADF + aire AGF + aire FGH + aire HGE + aire HEC + aire CBE
Nous avons:
EB = 10 - 6.4 = 3.6 cm
AG = EB
GE = AB - (AG + EB) = AB - 2 x AG =
10 - 2 x 3.6 = 10 - 7.2 = 2.8
L'aire de 3.6 x 10/2 + 3.6 x 10/2 + 2.8 x 10/2 + 2.8
x 10/2 + 3.6 x 10/2 + 3.6 x 10/2 = 100 cm2
Exemple 3
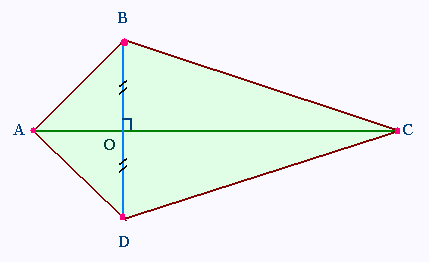
Aire du triangle ABC = (AC x OB)/2
Aire du triangle ADC = (AC x OD)/2
Nous avons OD = OB = 20 cm
AC = 80 cm
Les triangles ABC et ADC sont isométriques.
L'aire du cerf-volant est égale au double
de l'aire d'un triangle =
2 x (Aire du triangle ABC) = AC x OB =
80 x 20 = 1600 cm2 = 0.16 m2.
Exemple 4
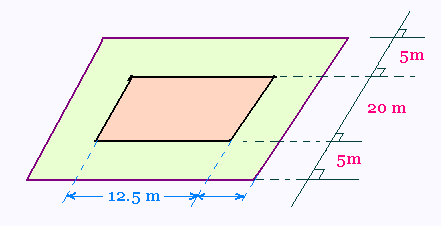
L'aire de la surface entre les deux parallélogrammes est
égale à l'aire du plus grand moins celle du petit.
= (17.5 + 2 x 5)x 30 - (20 x 17.5) =
27.5 x 30 - 20 x 17.5 = 825 - 350 = 475 m2
Exemple 5
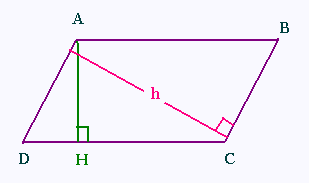
On donne:
DC = 9 cm, AH = 2.5 cm, et BC = 3 cm.
L'aire du parallélogramme ABCD est
égale à DC x AH = 9 x 2.5 = 22.5 cm2.
Cette aire est aussi égale à
BC x (hauteur relative au côté [BC]) =
[BC] x h
Donc
[BC] x h = 22.5 cm2
3 x h = 22.5
Donc
h = 22.5/3 = 7.5 cm.
Exemple 6
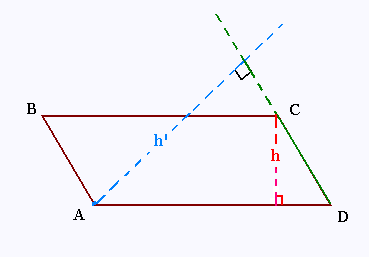
On donne:
AD = 18 cm, h = 3.6 cm, et h' = 12 cm.
L'aire du parallélogramme ABCD est
égale à [AD] x h = 18 x 3.6 = 64.8 cm2.
Cette aire est aussi égale à
[DC] x (hauteur relative au côté [DC]) =
[DC] x h'. Donc
[DC] x h' = 64.8 cm2
[DC] x 12 = 64.8
Il vient
[DC] = 64.8 /12 = 5.4cm.
Exemple 7
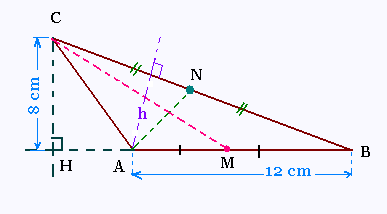
a) L'aire du triangle ABC est
égale à [AB] x [CH] /2 =
12 x 8 /2 = 48 cm2.
b) L'aire du triangle ACM est
égale à [AM] x [CH] /2 =
(12/2) x 8 /2 = 24 cm2.
c) Les aires des triangles ABN et ANC sont égales.
En effet, si on trace une hauteur "h" abaissée
du point A, l'aire du triangle ABN est égale à
[BN] x h /2 et celle du triangle ANC est
égale à [CN] x h /2.
Nous avons [BN] = [CN], donc
l'aire du triangle ABN est égale à
[BN] x h /2 = [CN] x h /2 = celle du
triangle ACN.
L'aire du triangle ABC est la somme
des aires des triangles ABN et ACN, et
donc au double du triangle ABN.
Ainsi l'aire du triangle ABN est égale à la moitié
de l'aire du triangle ABC.
L'aire du triangle ABN = 48/2 = 24 cm2.
Exemple 8
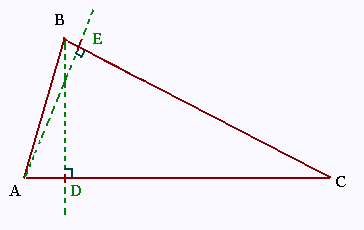
AC = 4.4 cm
BC = 4 cm
BD = 2.5 cm ( hauteur relative au côté [AC])
a)
L'aire du triangle ABC = [AC] x [BD] /2 =
4.4 x 2.5 = 11 cm2.
b) Cette aire est aussi égale à
[BC] x [AE] /2
Donc
[BC] x [AE] /2 = aire du triangle ABC =
11 cm2.
Il vient
[AE] = 2 x 11 /4 = 5.5 cm , qui est
la hauteur relative au côté [BC].
Exemple 9
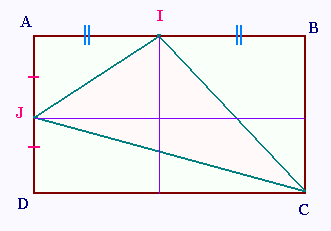
Le quadrilatère ABCD est rectangle de
dimensions 36 cm et 20cm.
[AB] = 36 cm et [BC] = 20 cm
L'aire du rectangle ABCD est :
[AB] x [BC] = 36 x 20 = 720 cm2.
L'aire du triangle AIJ est :
[AB]/2 x [AD]/2 = (36/2 x 20/2)/2 = 90 cm2.
L'aire du triangle JDC est :
[DC] x [AD]/2 = (36 x 20/2)/2 = 180 cm2.
L'aire du triangle IBC est :
[AB]/2 x [BC] = (36/2 x 20)/2 = 180 cm2.
L'aire du triangle IJC est égale à
l'aire du rectangle ABCD - l'aire des trois
triangles =
720 - 90 - 180 - 180 = 270 cm2.
Exemple 10
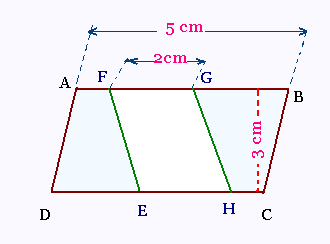
ABCD et EFGH sont des parallélogrammes.
L'aire du parallélogramme ABCD est égale à
5 x 3 = 15 cm2.
L'aire du parallélogramme EFGH est égale à
2 x 3 = 6 cm2.
L'aire des deux trapèzes qui restent est égale à
15 - 6 = 9 cm2.
Exemple 11
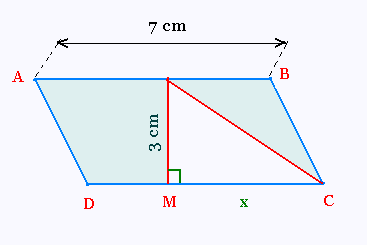
ABCD est un parallélogrammes. M est un point variable
sur le côté [DC].
x est la longueur MC en cm.
A est l'aire de la surface coloriée.
L'aire du parallélogramme ABCD est égale à
7 x 3 = 21 cm2.
a) x = 2 : L'aire du triangle est égale à
2 . 3 /2 = 3 cm2.
L'aire coloriée est égale à l'aire du
l'aire de parallélogramme - l'aire triangle =
21 - 3 = 18 cm2.
x = 3 : L'aire du triangle est égale à
3 . 3 /2 = 4.5 cm2.
L'aire coloriée est égale à l'aire du
l'aire de parallélogramme - l'aire du nouveau
triangle =
21 - 4.5 = 16.5 cm2.
b) On exprime A en fonction de x:
A = 21 - 3x/2
c) Si A = 12, alors
12 = 21 - 3x/2
3x/2 = 21 - 12 = 9
3x = 2 x 9 = 18
x 18/3 = 6 cm
Exemple 12
Définition
d’un Parallélogramme:
Un parallélogramme est un quadrilatère
convexe qui a ses côtés opposés isométriques.
Propriétés
d’un Parallélogramme
a) Des côtés:
Un parallélogramme a
ses côtés opposés parallèles et de même longueur.
c) Des angles:
Un parallélogramme a
ses angles opposés égaux, et ses angles successifs
supplémentaires
d) Des diagonales:
Les diagonales d'un parallélogramme se coupent
en leur milieu.
e) De symétrie:
Le point d'intersection des diagonales est
le un centre de symétrie. Le parallélogramme
n'a pas d'axe de symétrie.
Exemple 13
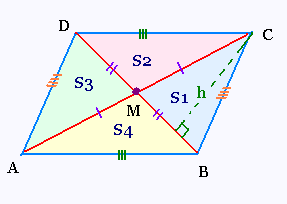
Le parallélogramme ABCD est formé de quatre
triangles.
L'aire du parallélogramme ABCD est égale la
somme des aires S1, S2, S3, et S4.
Les triangles ADC et ABC sont isométriques:
les aires de leurs surfaces sont égales:
S2 + S3 = S1 + S4
Les triangles BDC et ABD sont isométriques:
les aires de leurs surfaces sont égales:
S1 + S2 = S3 + S4
Les triangles AMD et BMC sont isométriques:
les aires de leurs surfaces sont égales:
S1 = S3
Les triangles AMB et DMC sont isométriques:
les aires de leurs surfaces sont égales:
S2 = S4
L'aire du triangle BMC est égale à
[BM] x h /2
L'aire du triangle DMC est égale à
[DM] x h /2
Avec [BM] = [DM], on trouve
L'aire du triangle BMC est égale à l'aire du triangle DMC. Ainsi
S1 = S2
Avec un même raisonnement pour les triangles
AMB et AMD, on trouve
L'aire du triangle AMB est égale à l'aire du triangle AMD. Ainsi
S3 = S4
Finalement
Les aires des quatres triangles formés par les diagonales d'un parallélogramme sont identiques
.
S1 = S2 = S3 = S4
|