Mathématiques 2: Géométrie
Polygones réguliers
Subdivision d'un heptagone

1. Subdivisions d'un polynome régulier

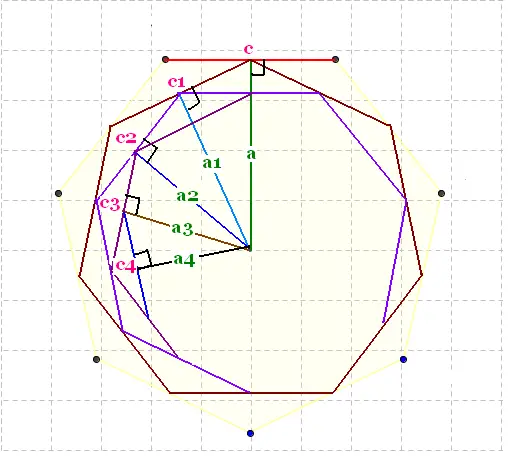
Nous avons un heptagone de côté c et d'apothème a.

En joignant les milieux des côtés de l'heptagone, on obtient un autre heptagone de côté c1 ar d'apothème a1.

Pour une deuxième subdivision, on obtient un autre deuxième heptagone de côté c2 et d'apothème a2,
et ainsi de suite, jusqu'à une m ième subdivision , on obtient alors un heptagone de côté cm et d'apothème am.

À chaque étape de subdivision, le rapport des côtés rest le même et est égal à k.

Nous allons donc calculer les cm et am pour une certaine valeur de m, calculer les aires des polygones subdivisés et ensuite la différence entre deux aires des polygones subdivisés succéssifs.

2. Calcul des côtés et des apothèmes

c₁ = k c (k < 1)
c₂ = k c1 = k² c
c₃ = k c2 = k³ c
c₄ = k c3 = k⁴ c
cm = k^m c

Le théorème de Pythagore mermet d'ecrire:

a₁² = a² - (c1/2)² =
a² - (1/4)(k²c² a2² = a1² - (c2/2)² =
a² - (1/4)(k²c² - (1/4)c² k⁴

a₃² = a₂² - (c3/2)² =
a² - (1/4)(k²c² - (1/4)c² k⁴ - (1/4)c² k⁶.

a₄² = a² - (1/4)k²c² - (1/4)c² k⁴ - (1/4)c² k⁶ - (1/4) c² k⁸.

...

a_m² = a² - (1/4)k²c² - (1/4)c² k⁴ - (1/4)c² k⁶ - (1/4) c² k⁸ - ... (1/4) c² k^2m =
a² - (1/4)c²[k² + k⁴ + k⁶ + k⁸ + ... + k^2m] =
a² - (1/4)c²k²[1 + k² + k⁴ + k⁶ + ... + k^{2m - 2}]

On utilise la somme de la série:

1 + x + x² + x³ + x⁴ + ... + x^s = (1 - x^{s + 1})/(1 - x)

Donc:

a_m² = a² - (1/4)c²k² [(1 - (k²)^{2m - 1})/( 1 - k²)]

Ainsi

pour m divisions d'un plygone de n côtés, on a:

c_m= k^m c
a_m = {a² - (1/4)c²k² [(1 - k^4m-2)/(1 - k²)]}^1/2

3. Calcul des aires

L'aire de m_e polygone est:
Am = n x a_m x c_m /2

L'aire du m_e+1 polygone est:
A_m+1 = n x a_m+1 x c_m+1/2

Leur différence est:
(n/2) [a_m x c_m - a_m+1 x c_m+1]

1. Application: heptagone

1 u = 1 unité = 1 cm,
n = 7
k = 0.9
c = 40 cm
a = 41.54 cm , et
m = 7 subdivisions

m	cm (u	am (u)	Am (u2)	Δ (u2)
1	36	43.76	5513.91	803.27
2	32.4	41.54	4710.63	685.99
3	29.16	39.43	4024.64	585.85
4	26.24	37.43	3438.79	500.33
5	23.62	35.5	2938.45	427.327
6	21.26	33.7	2511.12	364.96
7	19.13	32.05	2146.16	311.72

4. Relation entre le côté du polygone régulier et son apothème

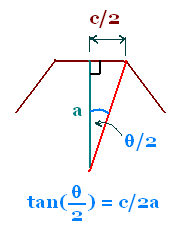
En fait, lorsque le polygone est régulier, il y a une relation entre son côté et son apothème, si l'un d'entre est connu, l'autre l'est aussi.

Si le polygone a n côtés, alors l'angle au centre de chaque triangle isocèle de base égale au côté du polygone est égal à 360°/n.

Soit θ = 360/n ,
"c" le côté du polygone et "a" son apothème.

θ/2 = 180°/n

tg (θ/2) = (c/2)/a , donc

a = c/(2 x tg(θ/2)) = c/2tg(180°/n)

a = c/(2 x tg(θ/2)) = c/2tg(180°/n) = c/2tg(π/n)

5. Relation entre les côtés des polygones subdivisés

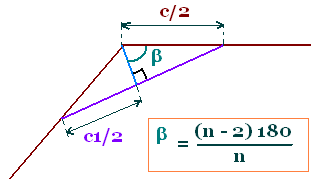
La somme S_n des mesures des angles intérieurs du polygone est égale à (n - 2) x 180 ° . Donc la mesure d'un angle au centre est α_n = S_n/n = (n - 2)180°/n

Le rapport des côtés de deux polygones consécutifs est constant.

Soit k ce rapport, nous avons:

(c₁/2)/(c/2) = c1/c = sin β = sin ((n - 2) 180/n)

k = sin ((n - 2) 180/n)

k = sin ((n - 2) 180/n)

Ce rapport ne dépend que de n.