Mathématiques 45: Géométrie
Formule de Héron
La formule de Héron donne l'aire d'un
triangle quelconque en fonction juste
des dimensions de ses trois côtés.
1. Formule de Héron
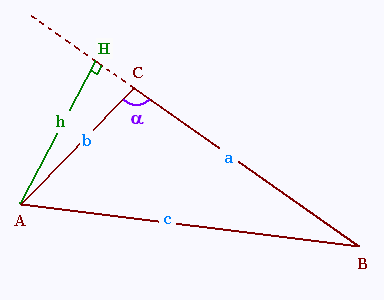
ABC est un triangle quelconque.
Son aire est égale à
A = (BC x AH)/2 =
(a x h)/2
Nous avons:
sin (180° - α) = h/b
sin (180° - α) = sin α
sin α = h/b
Donc:
h = b sin α
Il vient:
A = (a b sin α)/2 = (ab/2) sin α
A = (ab/2) sin α
La loi des cosinus permet d'ecrire:
c2 = a2 + b2 - 2ab cos α
D'où:
cos α = (1/2ab)(a2 + b2 - c2)
D'autre part,
sin2 α = 1 - cos2 α =
1 - (1/4a2b2)(a2 + b2 - c2)2
=
(1/4a2b2) x
[((2a)2b2) - (a2 + b2 - c2)2]
=
(1/(2ab)2) x
[((2ab)2) - (a2 + b2 - c2)2]
La différence des carrés donne:
((2ab)2) - (a2 + b2 - c2)2 =
[2ab + (a2 + b2 - c2)][2ab - (a2 + b2 - c2)]
=
[2ab + a2 + b2 - c2][2ab - a2 - b2 + c2)]
=
[(a + b)2 - c2)][c2 - (a - b)2]
=
[(a + b) + c][(a + b) - c][c - a + b][c + a - b]
=
(a + b + c)(a + b - c)(c - a + b)(c + a - b)
On pose:
S = (a + b + c)/2
Il vient:
S - a = (- a + b + c)/2
S - b = (a - b + c)/2
S - c = (a + b - c)/2
Ainsi:
(a + b + c)(a + b - c)(c - a + b)(c + a - b) =
(2S) 2(S - c) 2(S - a) 2(S - b) =
16 S (S - c)(S - a)(S - b)
Donc:
sin2 α =
(1/(2ab)2) x 16 S (S - c)(S - a)(S - b) =
4 S (S - c)(S - a)(S - b)/(ab)2 .
D'où:
sin α = 2 √[S (S - a)(S - b)(S - c)]/(ab)
L'aire du triangle ABC A = (ab/2) sin α devient:
A = (ab/2) x 2 √[S (S - c)(S - a)(S - b)]/(ab) =
√[S (S - c)(S - a)(S - b)]
Finalement,
A = √[S(S - a)(S - b)(S - c)]
S = (a + b + c)/2

C'est la formule de Héron .
2. Exemple 1
a) calculer l'aire du triangle de
dimensions suivantes:
a = 12 cm, b = 10 cm, c = 8 cm.
b) Utiliser la formule de Héron pour
trouver les inégalités triangulaires.
a)
S = (a + b + c)/2 = (12 + 10 + 8)/2 = 15 cm
A = √[S(S - a)(S - b)(S - c)] =
√[15(15 - 12)(15 - 10)(15 - 8)] =
√[15 x 3 x 5 x 7] = 15√7 = 39.69
A = 39.69 cm2
b) La radicante S(S - a)(S - b)(S - c)
doit être positive. C'est à dire:
S ≥ 0 → (a + b + c)/2 ≥ 0 → a + b + c ≥ 0
(S - a) ≥ 0 → (- a + b + c)/2 ≥ 0 → (b + c) ≥ a
(S - b) ≥ 0 → (a - b + c)/2 ≥ 0 → (a + c) ≥ b
(S - c) ≥ 0 → (a + b - c)/2 ≥ 0 → (a + b) ≥ c
Les trois dernières inégations représentent
les inégalités triangulaires.
2. Exemple 2
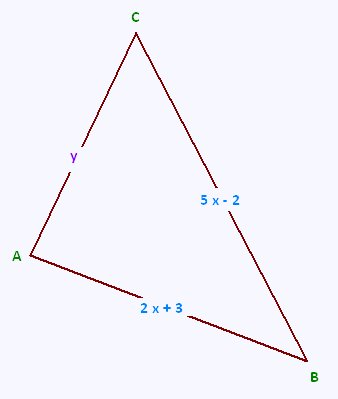
a) Calculer, en fonction de x, la valeur y du côté [A,C]
pour que le périmètre du triangle ABC soit égal à 21.
Pour x = 2, calculer:
b) Le périmètre du triangle ABC.
c) Les valeurs des côtés [AB], [AC], et [BC].
d) Le demi-périmètre S du triangle ABC.
e) Calculer son aire
f) Vérifier que ces trois côtés forment bien un triangle.
Héron d'Alexandrie

Héron d'Alexandrie est un ingénieur, mécanicien et mathématicien
grec du 1ier siècle après J.-C.
Il a vécu de la fin du premier siècle au dédut du 2eme siècle
après J.-C. sous l'Empire romain, en Alexandrie (Grèce).
On attribue à Héron d'Alexandrie plusieurs formules mathématiques.
La formule de Héron correspond à la méthode de calcul de l'aire d'un triangle
sans utiliser de hauteur, mais qui a déjà été prouvée par Archimède
(287 - 212 av. J.-C.).
On attribue aussi à Héron la formule dite la Méthode de Héron qui
permet d'approcher la racine carrée d'un nombre de manière récursive,
mais elle était déjà connue des Babyloniens
(2000 - 539 av. J.-C).
 Extraire une racine carrée: Méthode de Héron Extraire une racine carrée: Méthode de Héron
|