Maths
- 2 -
Géométrie
© The scientific sentence. 2010
| |
|
Mathématiques 2: L'homothétie
L'homothétie est une transformation géométrique
comme la translation, la rotation ou la refléction.
1.Définition
L'homothétie est une transformation géométrique qui
associe à chaque point initial un autre
point image à partir d’un point fixe
appelé centre d'homothétie suivant un facteur
appelé rapport d'homothétie.
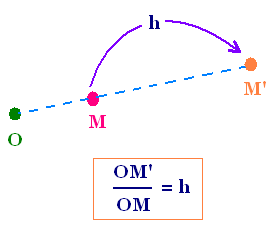
Donc, pour une figure qui est un ensemble de points,
L'homothétie est une transformation géométrique qui
associe à chaque figure initiale une autre
figure image à partir d’un point fixe
appelé centre d'homothétie suivant un facteur
appelé rapport d'homothétie.
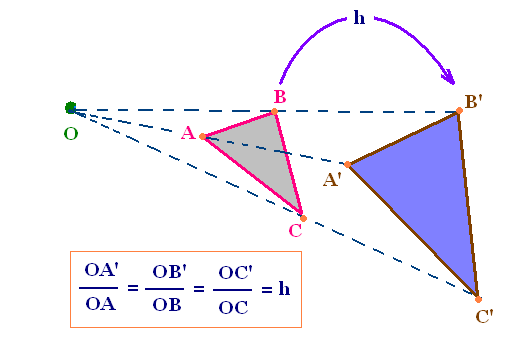
Le triangle A'B'C' est l'image du triangle ABC
par l'homothétie de contre O et de rapport h = 2.
Dans une homothétie, l'image d'un point est située
sur la droite passant par ce point et le centre
d'homothétie.
On utilise le symbol h pour désigner une
homothétie.
Mesure de la distance OA'
h = -------------------------
Mesure de la distance OA
2. Propriétés d'une homothétie
Lorsque le rapport d'homothétie est:
-- Compris entre 0 et 1, la figure image correspond
à une réduction de la figure initiale.
-- Égal à 1, la figure image est isométrique
à la figure initiale. C'est à dire, la figure image est
une reproduction exacte de la figure initiale.
-- Supérieur à 1, la figure image correspond
à un agrandissement de la figure initiale.
-- Si le rapport d'homothétie est positif : la figure
initiale et son image sont du même côté du centre d'homothétie O.
-- Si le rapport d'homothétie est négatif : la figure initiale et son
image sont de part et d'autre du centre d'homothétie O.
-- Si le rapport d'homothétie est égal - 1: la figure initiale
et son image sont symétriques par rapport au centre d'homothétie O.
L'homothétie est une transformation qui permet
d'obtenir des figures ayant:
-- Les angles homologues isométriques
-- Les côtés homologues parallèles
-- Les mesures des côtés homologues proportionnelles.
3. Exercices
1.
Dans chacun des cas donner le papport d'homothétie
de centre O.
__ __
OA = 3 cm 0A' = 18 cm
__ __
OA = 2,5 cm 0A' = 6.25 cm
__ __
OA = 1.1 mm 0A' = 3,3 cm
__ __
OA = 3 m 0A' = - 6 m
__ __
OA = 0.5 cm 0A' = - 1 cm
__ __
OA = 4 cm 0A' = - 2 cm
2.
Si un rectangle initial mesure 4 cm
de largeur et 12 cm de longueur, quelles
seront les mesures de la longueur et de la largeur
images tranformés par un homothétie de centre
O et de rapport h = 0.75?
3.
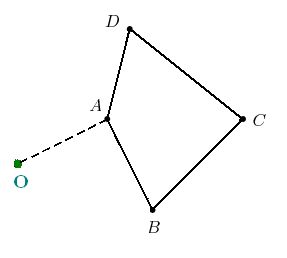
Représenter le quadrilatère image du quadrilatère
suivant selon un homothétie de centre O et de rapport h = - 4/7
Solutions
|
|