Mathématiques 45: Géométrie:
Loi des sinus et des cosinus
1. Loi des sinus
On utilise la loi des sinus:
. lorsque l'on connaît 2 angles et 1 côté qui
n'est pas compris entre ces angles,
. lorsque l'on connaît 2 côtés et 1 angle
qui n'est pas formé par ces deux côtés.
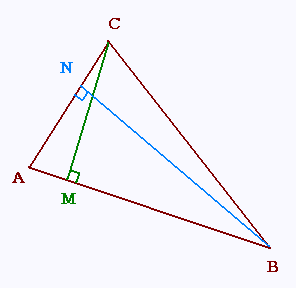
Une hauteur issue du point C permet
d'ecrire:
sin A = MC/AC → MC = AC sin A
sin B = MC/BC → MC = BC sin B
Donc AC sin A = BC sin B
AC/sin B = BC/sin A
Une hauteur issue du point B permet
d'ecrire:
sin C = BN/BC → BN = BC sin C
sin A = BN/AB → BN = AB sin A
Donc AB sin A = BC sin C
AB/sin C = BC/sin A
De même, une hauteur issue du point A permet
d'ecrire:
AC/sin B = AB/sin C
Ces trois relations sont groupées en une seule:
AC/sin B = BC/sin A = AB/sin C
2. Loi des cosinus
On utilise la loi des cosinus:
. Lorsque l’on cherche un angle connaîssant
les mesures de 3 côtés,
. Lorsque l’on cherche un côté connaîssant
la mesure d'un angle et celles de 2 côtés,
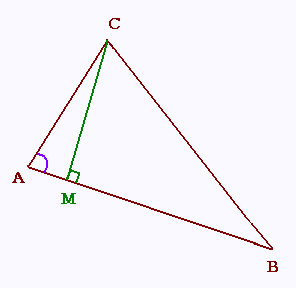
cos A = AM/AC d'où:
AM = AC cos A
MC2 = AC2 - AM2
BC2 = MC2 + BM2 =
MC2 + (AB - AM)2 =
AC2 - AM2 + (AB - AM)2 =
AC2 - AM2
+ AB2 + AM2 - 2(AB)(AM) =
AC2 + AB2 - 2(AB)(AM) =
AC2 + AB2 - 2(AB)(AC) cos A
BC2 = AC2 + AB2
- 2(AB)(AC) cos A
Une même démonstration avec une hauteur
isuue du sommet A et une hauteur issue du sommet B
donne les formules similaires suivantes:
AC2 = AB2 + BC2 -
2(AB)(BC) cos B
AB2 = AC2 + BC2 -
2(AC)(BC) cos C
Ces trois relations sont groupées en une seule:
BC2 = AC2 + AB2
- 2(AB)(AC) cos A
AC2 = AB2 + BC2 -
2(AB)(BC) cos B
AB2 = AC2 + BC2 -
2(AC)(BC) cos C
Dans un triangle quelconque, le carré de la mesure
d’un côté est égale à la somme des carrés des
mesures des deux autres côtés moins le double produit
des mesures des deux autres côtés et du cosinus de l’angle
compris entre ces deux côtés.
3. Exemples
Exemple 1:
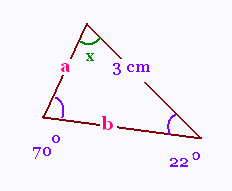
On connaît 2 angles et 1 côté qui
n'est pas compris entre ces angles:
On applique la loi des sinus:
a/sin 22 = 3/sin 70 = b/sin x
x = 180 - (70 + 22)
x = 86°
3/sin 70 = 3.20
b = 3.20 x sin 86 = 3.20 cm
a = 3.20 x sin 22 = 1.20 cm
Exemple 2:
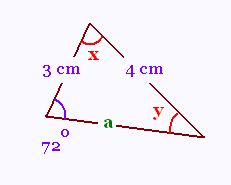
On connaît 2 côtés et 1 angle
qui n'est pas formé par ces deux côtés.
On applique la loi des sinus:
4/sin 72 = 3/sin y = a/sin x
4/sin 72 = 4.20
3/sin y = 4.20 → sin y = 0.71
y = 45.5°
x = 180 - (72 +45.5 ) = 62.5°
x = 62.5°
a/sin x = 4.20
a/sin(62.5) = 4.20
a = 4.20 x sin(62.5)
a = 3.72 cm
Exemple 3:
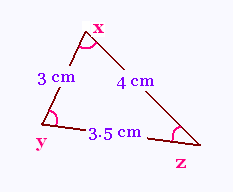
On connaît 3 côtés, et on cherche un angle.
On applique la loi des cosinus:
32 = 42 + (3.5)2 -
2(4)(3.5)cos z
cos z = (16 + 12.25 - 9)/2(4)(3.5) = 0.69
D'où:
z = 46.57 °
(3.5)2 = 32 + 42 -
2(4)(3)cos x
cos x = (16 + 9 - 12.25)/2(4)(3) = 0.53
D'où:
x = 57.90 °
y = 180 - (46.57 + 57.90)
y = 75.52°
On peut calculer la mesure des angles
x et y de la même façon.
Exemple 4:
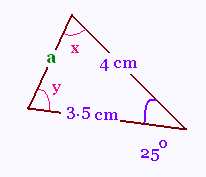
On cherche un côté connaîssant
la mesure d'un angle et celles de 2
autres côtés.
On applique la loi des cosinus:
a2 = 42 + 3.52 -
2(4)(3.5)cos 25°
a2 = 2.87
a = 1.70 cm.
On peut calculer la mesure des 2 autres angles
x et y avec la loi des cosinus:
3.52 = 42 + (1.70)2 -
2(4)(1.70)cos x
cos x = (16 + 2.87 - 12.25)/2(4)(1.70) = 0.049
x = 87.21°
y = 180 - (25 + 87.21 ) = 67.79
y = 67.79°
|