Maths
- 2 -
Géométrie
© The scientific sentence. 2010
| |
|
Mathématiques: Géométrie
Les lunules d'Hippocrate de Chios
Hippocrate de Chios est né à Chios vers - 470, et mort vers - 410.
Hippocrate est un mathématicien grec. À Athènes en - 430 a, ses interêts en Géométrie
commencèrent sur la quadrature du cercle. Il écrivit le premier ouvrage d’éléments
de géométrie connu, un siècle avant Euclide.
Il détermina l’aire de lunules, la proportion des surfaces de deux cercles
et les carrés de leurs rayons. Il étudia le problème de la duplication du cube.
Pour obtenir les lunules d'Hippocrate ,
on trace les trois demi-cercles de diamètres les
côtés d'un triangle rectangle.
Un calcul d'aire montre que l'aire du riangle rectangle
est égal à la somme des aires des deux lunules.
En géométrie, une lunule est une surface sous forme de croissant de lune
délimitée par deux cercles non concentriques de rayons différents.
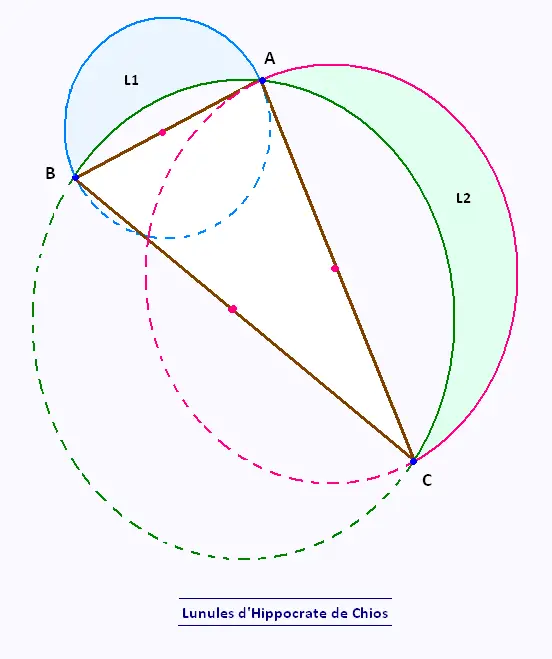
ABC est un triangle rectangle .
L'aire du demi-cercle de diamète [AB] est égale à
(1/2) π AB2/4 =
π AB2/8
L'aire du demi-cercle de diamète [AC] est égale à
(1/2) π AC2/4 =
π AC2/8
L'aire du demi-cercle de diamètre l'hypoténuse [BC] est égale
à
(1/2) π BC2/4 =
π BC2/8
Nus avons:
L'aire du demi-cercle de diamètre l'hypoténuse [BC] = L'aire du triangle ABC +
(l'aire du demi-cercle de diamète [AB] - L1) + (l'aire du demi-cercle de diamète [AC] - L2)
C'est à dire:
π BC2/8 = L'aire du triangle ABC + π AB2/8 - L1 +
π AC2/8 - L2
Or d'après la propriété de Pythagore:
AC2 = AB2 + AC2. D'où:
π BC2/8 = π AB2/8 + π BC2/8
Il vient donc:
0 = L'aire du triangle ABC - L1 - L2, ou
L'aire du triangle ABC = L1 + L2
L'aire du triangle rectangle ABC = L1 + L2
|
|