Mathématiques: Géométrie
L'alignement des points

Propriétés des points alignés

• Trois points ou plus sont alignés lorsqu'ils sont situés sur une même droite.


• Si les points A, B et C forment un angle plat, alors ces trois point sont alignés.

• Si trois points A B et C forment l'angle nul ABC, alors les points A B et C sont alignés.

• Si (AB) est parallèle à (d) et (AC) est parallèle à (d). Comme A est un point commun à ces deux droites, alors elles sont confondues et A, B et C sont alignés.


• Si (AB) est perpendiculaire à (d) et (AC) est perpendiculaire à (d). Comme A est un point commun à ces deux droites, alors elles sont confondues et A, B et C sont alignés.

• Le milieu M d'un segment [AB] est aligné avec les extrémités A et B de ce segment.

• Si la somme des distances AC et CB est égale à la distance AB alors les points A, B et C sont alignés.

• Si la somme des distances AC et CB est égale à la distance AB alors les points A, B et C sont alignés.

Si AC + CB = AB ↠ A, B, C sont alignés.

• L'alignement conserve la symétrie axiale.

• L'alignement conserve la symétrie centrale.

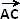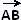• Si le vecteur est colinéaire (ou proportionnel) au vecteur, comme A est un point commun à ces deux vecteurs, alors les trois points A, B et C sont alignés.

• Si les droites (AB) et (AC) ont une même pente (coefficient directeur ou taux de variation), comme A est un point commun à ces deux droites, alors les points A, B et C sont alignés.

• Un point, le centre de symétrie centrale, et le symétrique du point par rapport à ce centre sont alignés.

• Un point, le pieds de la symétrie axiale , et le symétrique du point par rapport à cet axe sont alignés.