Mathématiques 2: Polyèdres
1. Définitions
1.1. Polyèdre
Un solide est une portion d'espace limitée
par une surface fermée.
Un polyèdre est un solide limité par des
faces planes formées par des polygones.
Le développement d'un polyèdre est la figure
plane obtenue par un mise à plat de sa surface; dont
chacune des faces est relié à au moins une autre
face par une arête commune.
1.2. Prisme
Un prisme est une polyèdre formé par deux
faces isométriques et parallèles appelées bases.
Les parallélogrammes qui relient ces deux bases sont
appelés des faceslatérales
Un prisme est droit si ses faces
latérales sont des rectangles.
Un prisme est régulier s'il est droit
et en plus sa base est un polygone régulier.
La hauteur d'un prisme droit est la distance entre
les deux bases du prisme.
1.3. Pyramide
Une pyramide est polyèdre formé d'une seule base
et dont les faces latérales sont des triangles. Ces
triangles ont un même sommet commun appelé apex.
Une pyramide est droite si la hauteur abaissée
à partir de l'apex se trouve au milieu de la base.
Une pyramide est régulière si elle droite et en
plus sa base est formée d'un polygone régulier.
La hauteur d'une pyramide droite est la distance entre
l'apex et la base de la pyramide.
2. polyèdres réguliers
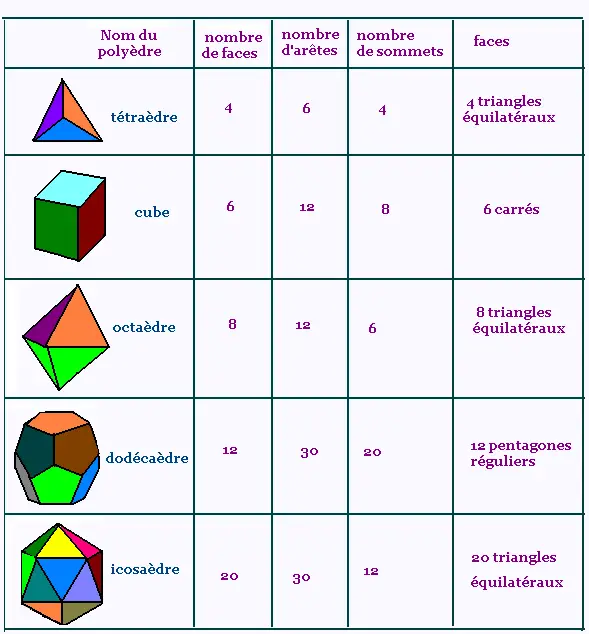
3. Développement d'un polyèdre
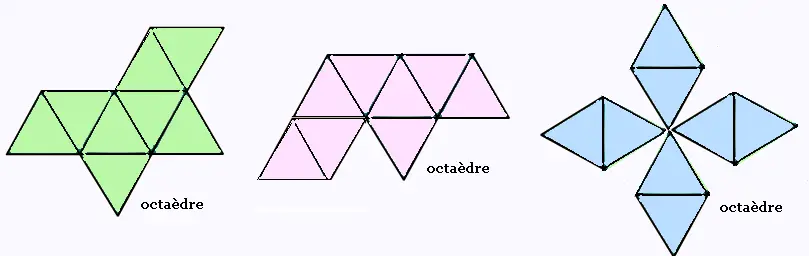
3.1. Octaèdre
Voici trois parmi les 11 façons de développer
un octaèdre:
3.2. Dodécaèdre
Développement d'un dodécaèdre:
4. Exemples
4.1. Prisme régulier à base pentagonale
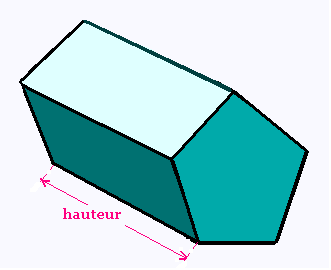
Cette "chose" est un solide puisqu'il occupe un
espace limité par une surface fermée qui est formée
par ses deux bases et sa surface latérale.
Cette surface fermée est constituée de faces planes
formées par des polygones, ce solide est donc un
polyèdre.
Ce polyèdre est un prisme puisque ses bases sont
isométriques et parallèles. Ses faces latérales sont
des rectangles, ce prisme et donc droit. En plus
sa base est un polygone régulièr; le prisme
est donc régulier.
4.2. Pyramide régulière à base pentagonale
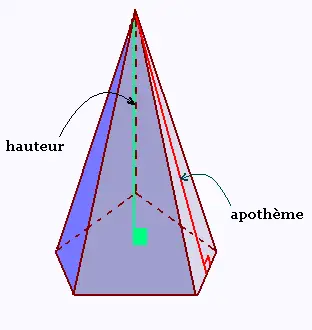
Cette "chose" est un solide puisqu'il occupe un
espace limité par une surface fermée qui est formée
par sa base et sa surface latérale.
Cette surface fermée est constituée de faces planes
formées par des polygones, ce solide est donc un
polyèdre.
Ce polyèdre est une pyramide puisqu'il est formé
d'une seule base polygonale et de faces latérales qui
sont des triangles ayant un apex. Cette pyramide est droite
puisque la hauteur abaissée depuis l'apex rencontre
la base en son milieu. En plus cette base est un polygone
régulier. La pyramide est donc régulière.
5. Exercice
5.1. Question
Voici un polyèdre régulier:
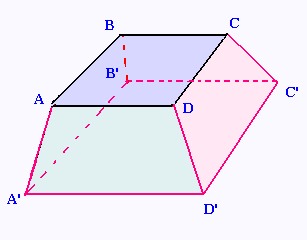
ABCD est la section d'une pyramide
Cette section est obtenue en coupant une grande
pyramide à base carrée parallèlement à sa base.
La section ABCD reste donc carrée.
En coupant la pyramide, on obtient aussi:
- une petite pyramide à base carrée OA'B'C'D' et
- un polyèdre régulier qui n'est pas
une pyramide ni un prisme.
a) Placer dans une figure la pyramide OABCD qui
résulte de la coupe de la pyramide OA'B.C'D'.
b) Donner la signification du point O
c) Calculer l'aire totale de la grande pyramide
OABCD.
On donne:
A'D' = 10 cm
AD = 8 cm
DD' = 4 cm
5.2. Réponse
a)
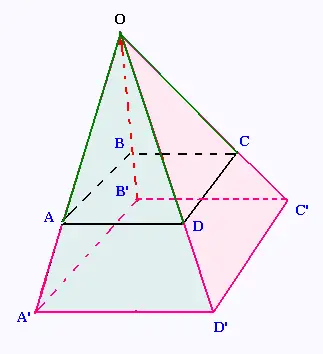
Rappels:
Rappel 1:
La section d'un solide est la face obtenue par
un plan qui coupe ce solide.
Rappel 2:
L'homothétie est une transformation géométrique qui associe
à toute figure initiale une figure image selon un point fixe
appelé centre d'homothétie, et un rapport
appelé rapport d'homothétie.
Dans une homothétie, l'image d'un point est située sur
la droite passant par ce point et le centre d'homothétie.
L'homothétie est une transformation qui permet d'obtenir
des figures ayant:
- des angles homologues isométriques
- des côtés homologues parallèles
- des mesures des côtés homologues proportionnelles
Deux figures sont semblables si l'une est un agrandissement,
une réduction, ou la reproduction exacte de l'autre.
Dans deux figures semblables:
- les angles homologues sont isométriques
- Les mesures des côtés homologues proportionnelles
Le rapport de smilitude est égal à
(mesure d'un côté de la figure image)/(mesure du côté
homolgue de la figure initiale).
b)
Le point O le centre d'homothétie.
c)
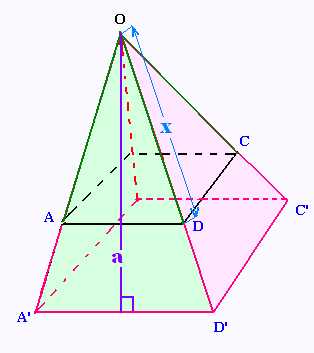Soit x la mesure du côté oblique OD.
Le rapport de similitude des triangles OAD et OA'D'
s'ecrit:
x/(x + DD') = OA/OA' = AD/A'D'
x/(x + 4) = 8/10 = 4/5
On résout pour x
x/(x + 4) = 4/5 → 5 x = 4(x + 4) = 4 x + 16
x = 16 cm.
Par conséquent
OD' = OD + DD' = 16 + 4 = 20 cm.
OD' = 20 cm.
Soit "a" l'apothème de la grande pyramide.
Le théorème de Pythagore permet d'ecrire:
a2 + (A'D'/2)2 = (OD')2
a2 + (10/2)2 = (20)2
a2 = 400 - 25 = 375
a = 19.36 cm
a = 19.36 cm.
L'aire latérale de la grande pyramide est égale à
Al = 4 x 19.36 x 5 /2 = 193.6 cm2
L'aire de la base de la grande pyramide est égale à
Ab = 10 x 10 = 100 cm2
L'aire totale de la grande pyramide est égale à
A = Al + Ab = 193.6 + 100 = 293.6 cm2
L'aire totale de la grande pyramide est égal à 293.6 cm2.
|
