Mathématiques 2: Polygones
1. Definition
Un polygone est une figure géométrique dans
un plan qui possède plusieurs côtés. Un terrain de
soccer est un polygone.
Un polyèdre est une corps géométrique dans l'espace
à trois dimensions qui possède plusieurs faces planes
polygonales.
Une pierre précieuce, comme le diamond,
taillée en une dizaine de facettes est
un polyèdre.
2. Polygones particuliers
un polygone particulier ou polygone simple
est un polygone pour lequel on sait calculer son aire.
Les polygones particuliers sont:
-- Le triangle
-- Le rectangle
-- Le losange
-- Le trapèze
-- Le parallélogramme
-- Les poygones réguliers
3. Polygone régulier
Un polygone régulier est un polygone équilatéral.
C'est à dire tous ses côtés sont égaux et tous les angles
sont égaux.
Un triangle equilatéral, un carré, un pentagone
sont des polygones réguliers.
Un rectangle, un losange ne sont pas des polygones
réguliers.
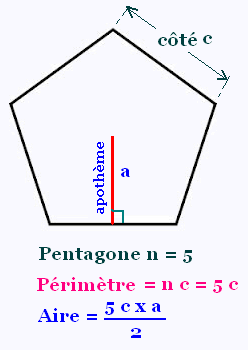Le périmètre d'un polygone régulier est égal au
nombre n des ses côtés multiplié par son côté c.
P = n c
L'aire d'un polygone régulier est égale à la moitié
du produit de son périmètre et de son apothème:
Aire = (perimètre) x (apothème)/2
L'aire d'un polygone régulier est égale à
la moitié du produit de son côté "c", de son
apothème "a" et du nombre "n" de ses côtés:
Aire = c a n/2.
|
|
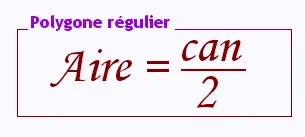
4. polygones décomposables
Une polygone décomposable se décompose en plygones
simples.
Pour calculer l'aire d'un polygone décomposable, on calcule
l'aire de ses plygones simples et on procède par addition ou
soustraction.
5. Exemple
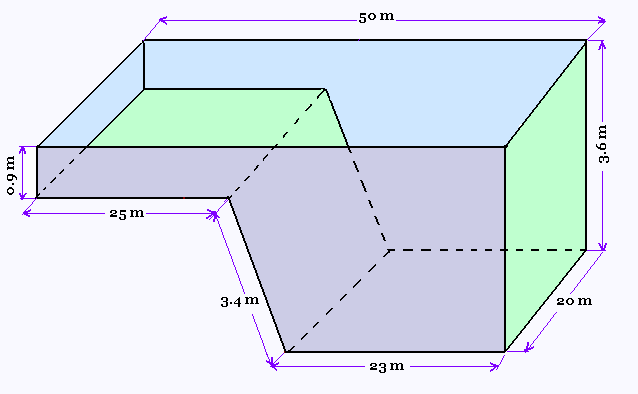L'aire de la surface intérieure de la piscine est égale
à la somme des aires des surfaces en largeur et du double
de la surface en longeur sans le trapèze formé par
la dénivellation.
20 x (3.6 + 23 + 3.4 + 25 + 0.9) +
2 [50 x 3.6 - (50 - 23 + 25) x (3.6 - 0.9)/2] =
20 x (55.9) + 2 [180 - 52 x 2.7/2] =
1118 + 360 - 156 + 15.6 = 1337.6 m2
6. Exercices
6.1. Exercice 1
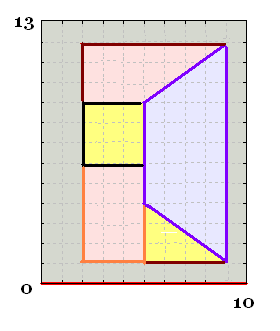Dans ce rectangle de 10 x 13 cm , nous avons
un bloc formé de polygones simples.
a) Calculer l'aire du bloc
b) calculer l'aire qui n'est pas occupée
par le bloc.
6.2. Exercice 2
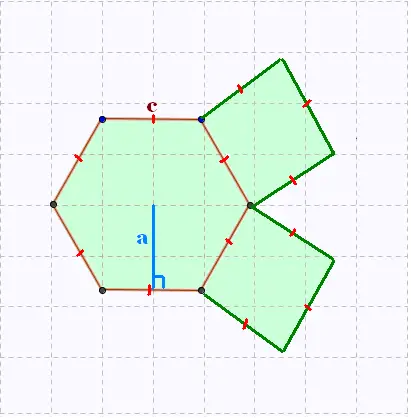Quelle est la mesure du côté de l'hexagone,
qui est en même temps le côté du carré, si
la somme des aires de l'hexagone et des deux
carrés est égale à 226.1 cm2?
L'apothème mesure 6.1 cm.
Solutions
|
